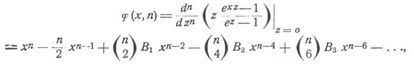Bernoullische Zahlen und Funktionen
- Bernoullische Zahlen und Funktionen
Bernoullische Zahlen und Funktionen. Die Bernoullischen Zahlen B1, B2, B3, B4, ... (früher bezeichnete man sie mit B1, B3, B5, B7, ..., während man B2, B4, B6, ... gleich Null annahm) sind gewisse positive rationale Brüche, die bei zahlreichen Reihenentwicklungen auftreten (Beispiele s. Goniometrie,
[710] Hyperbelfunktionen und Reihen). Sie werden von der vierten an immer größer, und zwar nehmen sie zuletzt schneller zu als die Glieder einer jeden wachsenden geometrischen Reihe.
Es ist z.B. B1 = 1/6, B2 = 1/30, B3 = 1/42, B4 = 1/30, B5 = 5/66, B6 = 691/2730. Die Werte der 32 ersten Bernoullischen Zahlen findet man auf der letzten Seite von [2]. – Die nte Bernoullische Funktion, φ(x, n), ist eine gewisse ganze rationale Funktion nten Grades von x, nämlich:
wobei die rechte Seite mit dem die Potenz x2 oder x enthaltenden Gliede abschließt. – Weitere Eigenschaften und Literatur in [3].
Literatur: [1] Schlömilch, O, Kompendium der höheren Analysis, Bd. 2, 3. Aufl., Braunschweig 1879. – [2] Saalschütz, L., Vorlesungen über die Bernoullischen Zahlen, Berlin 1893. –,[3] Encyklopädie der mathem. Wissensch., Bd. 2, I, Leipzig 1900, S. 181 ff.
Mehmke.
http://www.zeno.org/Lueger-1904.
Schlagen Sie auch in anderen Wörterbüchern nach:
Bernoullische Zahlen — Die Bernoulli Zahlen Bn sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler Maclaurin Formel, und … Deutsch Wikipedia
Bernoullische Zahl — Die Bernoulli Zahlen Bn sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler Maclaurin Formel, und … Deutsch Wikipedia
Bernoulli-Zahlen — Die Bernoulli Zahlen Bn sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler Maclaurin Formel, und … Deutsch Wikipedia
Euler-Mascheroni-Konstante — γ Die Euler Mascheroni Konstante (nach den Mathematikern Leonhard Euler und Lorenzo Mascheroni), auch Eulersche Konstante, ist eine wichtige mathematische Konstante, die mit dem griechischen Buchstaben γ (Gamma) bezeichnet wird … Deutsch Wikipedia
Konkave Funktion — Konvexe Funktion In der Analysis heißt eine Funktion f von einem Intervall I (oder allgemeiner einer konvexen Teilmenge C eines reellen Vektorraums) nach … Deutsch Wikipedia
Konvexe Funktion — In der Analysis heißt eine Funktion f von einem Intervall I (oder allgemeiner einer konvexen Teilmenge C eines reellen Vektorraums) nach … Deutsch Wikipedia
Bernoulli-Polynom — Die Bernoulli Zahlen Bn sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler Maclaurin Formel, und … Deutsch Wikipedia
Bernoulli-Polynome — Die Bernoulli Zahlen Bn sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler Maclaurin Formel, und … Deutsch Wikipedia
Bernoullipolynom — Die Bernoulli Zahlen Bn sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler Maclaurin Formel, und … Deutsch Wikipedia
Bernoullizahl — Die Bernoulli Zahlen Bn sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler Maclaurin Formel, und … Deutsch Wikipedia