Geradführung, absolute

Geradführung, absolute. Wird vermittelst eines Mechanismus (s.d.), dessen Glieder durch Achsengelenke beweglich verbunden sind, eine geradlinige Bewegung erzeugt, so heißt dieselbe eine absolute Geradführung.

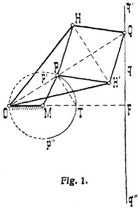
Man hat es lange Zeit für unmöglich gehalten, daß durch einen Gelenkmechanismus, bei dem also jedes Glied gegen ein benachbartes eine Kreisbewegung vollzieht, eine geradlinige Bewegung erzeugt werden könne, bis von Peaucellier [1] zuerst der in Fig. 1 schematisch dargestellte Gelenkmechanismus erfunden wurde, durch den eine absolute Geradführung bewirkt wird. Dieser Peaucelliersche Mechanismus besteht aus acht Gliedern, die durch sechs parallele Achsengelenke verbunden sind. Das Glied M O ist fest und als solches durch eine Schraffur von den beweglichen Gliedern unterschieden. Um die feste Achse O drehen sich die beiden gleichlangen Glieder OH, OH', die in H, H' mit einem Gelenkrhombus P H Q H' gelenkig verbunden sind; um die feste Achse M dreht sich das Glied M P, das gleich M O und in P drehbar an diesen Gelenkrhombus angeschlossen ist. Die sechs Gelenke, deren Achsen senkrecht zur Zeichnungsebene sind, werden durch die betreffenden Punkte in der Zeichnung vertreten. Wird nun das Glied M P gedreht, dann bewegt sich der Gelenkpunkt Q in bezug auf das feste Glied M O in einer auf M O senkrechten Geraden q. Einer Schwingung von M P entspricht eine Bewegung des Gelenkpunktes Q auf einer Strecke der Geraden q. Der Beweis für diese absolute Geradführung ergibt sich durch die folgende Betrachtung. Die Punkte O P Q liegen, weil H O H', H P H', H Q H' gleichschenklige Dreiecke sind, stets auf einer Geraden, die in der Mitte auf der veränderlichen Strecke H H' senkrecht steht. Setzen wir die Länge der gleichlangen Glieder O H, O H' gleich a, die Länge der vier gleichen Rhombusseiten gleich b, und denken wir uns um H den durch P, Q gehenden Kreis beschrieben, so ist nach einem geometrischen Satze das Produkt O P · O Q = (a – b) (a + b) = a² – b²;[398] also konstant. Der um M mit dem Radius M P = r beschriebene Kreis geht durch O, weil M P = M O ist, und schneidet ferner die Gerade O M in einem Punkt T; die durch Q auf O M senkrechte Gerade q schneidet O M im Punkte F. Wegen der ähnlichen rechtwinkligen Dreiecke O P T, O F Q ist:

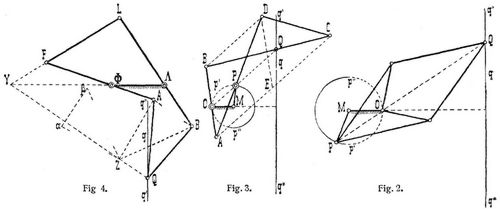
folglich bewegt sich der Punkt Q in einer auf O M senkrechten Geraden q, deren Abstand O F von O durch den erhaltenen Ausdruck bestimmt ist. Bei dem in Fig. 2 gezeichneten Peaucellierschen Mechanismus ist a < b, und die feste Achse O liegt dann zwischen P und Q. Für diese Anordnung ergibt sich O P · O Q = – (a² – b²). – Die Grenzlagen q', q'' des Punktes Q auf der Geraden q ergeben sich bei beiden Mechanismen dadurch, daß O q' = O q'' = a + b gemacht wird, und diesen entsprechen die Grenzlagen p', p'' des Punktes P auf dem durch O gehenden Kreise. Diese Punkte p', p'' liegen bezw. auf den Geraden O q' und O q''. Wenn also P auf dem größten zulässigen Bogen p' P p'' schwingt, bewegt sich der Punkt Q auf der Geraden q in der größten Hubhöhe q' q''. – Nachdem durch den Peaucellierschen Mechanismus das Problem der absoluten Geradführung gelöst war, welches man als unlösbar, wie die Quadratur des Zirkels, betrachtet hatte, wurden bald mehrere Gelenkmechanismen erfunden, die eine absolute Geradführung erzeugten. Hart [2] erfand den in Fig. 3 dargestellten sechsgliedrigen Mechanismus mit lieben Achsengelenken. Derselbe besteht aus einem Antiparallelogramm A B C D, auf dem die drei Punkte O P Q in einer zu A C bezw. B D parallelen Geraden liegen; ferner aus dem festen Gliede O M mit der festen Achse O, um die sich die Seite A B des Antiparallelogramms dreht, und dem Gliede M P = M O, das sich um die feste Achse M dreht und in P gelenkig mit der Seite A D des Antiparallelogramms verbunden ist. Wird nun das Glied M P gedreht, dann bewegt sich der Punkt Q des Gliedes B C in einer auf O M senkrechten Geraden q. Die drei Punkte O, P, Q teilen die Glieder A B, A D, C B in gleiche Verhältnisse und bleiben deshalb während der Bewegung stets in einer zu A C oder B D parallelen Geraden. Setzen wir die gleichen Gliedlängen A B, C D gleich a und die gleichen Gliedlängen A D, B C gleich b, so ist:

Ziehen wir die Gerade D E, die A C in E trifft, parallel zu B A, dann ist: A C · B D = A C · A E = b² – a². Hiernach ist das Produkt O P · O Q = A O · B O · b² – a²/a² konstant; und es folgt demnach in gleicher Weise, wie oben begründet wurde, daß der Punkt Q sich in einer auf O M senkrechten Geraden q bewegt, wenn das Glied M P gedreht wird. Die Grenzlagen q', q'' des Punktes Q auf der Geraden q ergeben sich dadurch, daß O q' = O q'' = O B + B Q gemacht wird, und diesen entsprechen die Grenzlagen p', p'' des Punktes P auf dem durch O gehenden Kreise. Die Punkte p', p'' liegen bezw. in der Geraden O q' und O q''. Von Sylvester [3] und Kempe [4] wurde dieser Mechanismus gleichzeitig verallgemeinert. Bei den betrachteten Mechanismen entspricht einer schwingenden Bewegung auf einem Kreisbogen eine schwingende Bewegung auf einer Geraden.

Hart [5] hat aber auch einen andern, in Fig. 4 dargestellten sechsgliedrigen Mechanismus mit lieben Achsengelenken erfunden, durch den während einer vollen Umdrehung eine schwingende Bewegung auf einer Geraden erzeugt wird. Dieser Mechanismus, dessen Konstruktion hier noch ohne Beweis angegeben werden soll, besteht aus einem Doppelkurbelgetriebe (s.d.) Φ F L Λ, dessen Kurbeln Φ F, Λ L sich um die festen Achsen Φ, Λ des festen Gliedes Φ Λ herumdrehen, und an diesen Kurbeln sind die Glieder A Q, B Q eines Knies A Q B drehbar angeschlossen, dessen Gelenkpunkt Q während der Umdrehungen der beiden Kurbeln auf der Strecke q' q'' der auf Φ Λ senkrechten Geraden schwingt. Um diesen Mechanismus zu konstruieren, nehmen wir ein beliebiges Doppelkurbelgetriebe Φ F L Λ als gegeben an. Wir konstruieren die Mittelpunkte α, β der den Dreiecken Φ F Y und Λ L Y umschriebenen Kreise, deren zweiter Schnittpunkt Z ist, ziehen auf α Z die Senkrechte Z A, auf β Z die Senkrechte Z B und machen A Q = B Z, B Q = A Z. Hierbei liegt der Gelenkpunkt Q in der auf α β senkrechten Geraden Y Z, weil A B parallel Y Z ist, und es ist Φ A : Φ F = Λ B : Λ L [6]. Andre Mechanismen für absolute Geradführungen wurden von Kempe [7] angegeben.

[399] Literatur: [1] Peaucellier, Nouvelles annales de mathématiques, 1864, Ser. II, Bd. 3, S. 414; 1873, Sér. II, Bd. 12, S. 71. – [2] Hart, Messenger of Mathematics 1875, Bd. 4, S. 82. – [3] Sylvester, »Nature«, 15. Juli 1875, Bd. 12, S. 214. – [4] Kempe, »Nature«, 31. Mai 1877, Bd. 16, S. 88. – [5] Hart, Proceedings of the London Mathematical Society, 1877, Bd. 8, S. 288; Kempe, ebend., 1877, Bd. 9, S. 138. – [6] Burmester, Zeitschr. f. Mathematik und Physik, 1893, Jahrg. 38, S. 193, und Burmester, Lehrbuch der Kinematik, 1887, Bd. 1, S. 564, mit weiterer Literaturangabe. – [7] Kempe, Proceedings of the Royal Society of London, 17. Juni 1875, Bd. 23, S. 565; »Nature«, 14. Juni 1877, Bd. 16, S. 125.

Burmester.

Fig. 1.

Fig. 2., Fig. 3., Fig. 4.