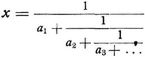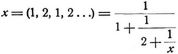Kettenbrüche

Kettenbrüche heißen Ausdrücke von der Form Ein solcher ist endlich oder unendlich, je nachdem x eine rationale oder irrationale Zahl ist.

Die Größen a₁ a₂ a₃... heißen Partialnenner; der Kettenbruch wird auch kurz geschrieben (a₁ a₂ a₃ ...). Alsdann werden die Brüche P₀/Q₀ = 1/0; P₁/Q₁ = 0/1; P₂/Q₂ = (a₁) = 1/a₁; P₃/Q₃ = (a₁ a₂) = 1/a₁ + 1/a₂ = a₂/a₁ a₂ + 1; P₄/Q₄ = (a₁ a₂ a₃) = (a₂ a₃ + 1)/(a₁ a₂ a₃ + a₁ + a₃) ... Näherungsbrüche genannt. Man erhält dieselben mittels der Rekursionsformeln: P_n = P_n–1.a_n–1 + P_n–2; Q_n = Q_n–1 a_n–1 + Q_n–2. Beispiel: ³⁷/₆₅ = (1, 1, 3, 9) Näherungsbrüche: P₀ = ∞; P₁ = 0; P₂ = 1; P₃ = ¹/₂; P₄ = ⁴/₇. Die Differenz zweier aufeinander folgenden Näherungsbrüche ist ein Bruch, dessen Zähler die Einheit und dessen Nenner das Produkt der Nenner der Näherungsbrüche ist, z.B. ⁴/₇ – ¹/₂ = ¹/₁₄. Die Reihe der Näherungsbrüche nähert sich immer mehr der Zahl x; sie sind abwechselnd größer und kleiner als x. Wird an Stelle von x ein Näherungsbruch gesetzt, so ist der begangene Fehler kleiner als die Einheit dividiert durch das Quadrat des Nenners des Näherungsbruchs, z.B. ³⁷/₆₆ – ¹/₂ = ⁹/₁₃₀ < ¹/₄. Jeder Näherungsbruch ist von x weniger verschieden als jeder andre Bruch, dessen Nenner kleiner ist als derjenige des Näherungsbruchs. – Die endlichen Kettenbrüche dienen zur Auflösung diophantischer Gleichungen (s.d.) und zur Ersetzung von Brüchen durch solche mit kleineren Zahlen. Ein unendlicher Kettenbruch heißt periodisch, wenn (von einer gewissen Stelle an) die Partialnenner eine immer wiederkehrende endliche Reihe bilden. Ein solcher Kettenbruch kann als irrationale Wurzel einer Gleichung zweiten Grads dargestellt werden, z.B.:

ist die positive Wurzel der Gleichung x² + 2 x – 2 = 0, also x = – 1 + √3.

Literatur: [1] Serret, Handbuch der höheren Algebra, deutsch von Wertheim, Bd. 1, 2. Aufl., Leipzig 1878, S. 7–70. – [2] Scheffler, Die unbestimmte Analytik, Hannover 1854. – [3] Kämpe, Die allgemeinen Kettenbrüche und ihre wichtigsten Eigenschaften, Siegen 1875.

Wölffing.