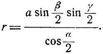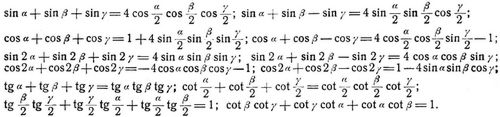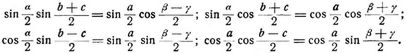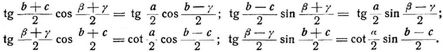- Trigonometrie
Trigonometrie, Ausmessung der Dreiecke und Berechnung derselben aus gegebenen Stücken. Zu diesem Zweck wird von den goniometrischen Funktionen der Winkel (s. Goniometrie) Gebrauch gemacht.
A. Ebene Trigonometrie. Seiten a, b, c, Winkel α, β, γ. α + β + γ = 180°.
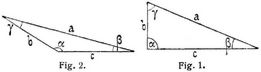
I. Rechtwinkliges Dreieck (Fig. 1). α sei rechter Winkel; β + γ = 90°. Es ist: b = a sin β = a cos γ; c = a cos β = a sin γ; b = c tg β = c cot γ; c = b tg γ = b cot β; a2 = b2 + c2.
II. Schiefwinkliges Dreieck (Fig. 2).
Sinussatz: a : b : c = sin α : sin β : sin γ.
Cosinussatz: a = b cos γ cos β (und die beiden hieraus durch cyklische Vertauschung von a, b, c; a, β, γ hervorgehenden Formeln).
Pythagoräischer Lehrsatz im schiefwinkligen Dreieck: a2 = b2 + c2 – 2 b c cos α.
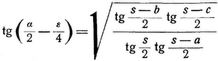
Mollweides Formeln:
Höhe hα = b sin γ = c sin β. Fläche: 1/2 a b sin γ. Radius des Umkreises R = α/2 sin α.
Radius des Umkreises
wo s = 1/2 (a + b + c).
Ferner ist
Sind α, β, γ die Winkel eines Dreiecks, so gelten die Formeln:
B. Sphärische Trigonometrie. Im sphärischen Dreieck sind die Seiten ebenfalls Winkelgrößen, nämlich Großkreisbögen; die Dreieckswinkel sind die Winkel der Ebenen dieser Großkreisbögen.
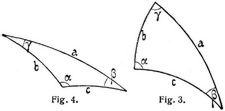
I. Rechtwinkliges Dreieck (Fig. 3). α sei der rechte Winkel. Es ist cos a = cos b cos c; sin b = sin a sin β; sin c = sin a sin γ; tg c = tg a cos β; tg b = tg a cos γ; tg b = sin tg β; tg c = sin b tg γ, cos a = cot β cot γ; cos β = cos b sin γ; cos γ = cos c sin β.
II. Schiefwinkliges Dreieck (Fig. 4). Cosinussatz: cos a = cos b cos c + sin b sin c cos α u.s.w.
Sinussatz: sin a : sin b : sin c = sin α : sin β : sin γ; sin a cos β = cos b sin c – sin b cos c cos α u.s.w. cos α = – cos β cos γ + sin β sin γ cos a u.s.w.
[622] Delambresche Gleichungen (Gaußsche Formeln):
Es sei ferner
der sogenannten Eckensinus oder die Amplitude des Dreiecks. Alsdann ist 2 S = sin a sin b sin c u.s.w.;
u.s.w. Die Größe ε = α + β + γ – 180° heißt sphärischer Exzeß. Die Dreiecksfläche verhält sich zur Kugelfläche wie der sphärische Exzeß zu 720°.
Gleichung von L'Huilier:
Ferner ist
u.s.w. Höhe sin ha = sin b sin γ = sin c sin β. Radius des Umkreises
Radius des Umkreises
Berechnung der ebenen und sphärischen Dreiecke s. Dreiecksberechnung.
C. Sphäroidische Trigonometrie heißt die Ausmessung der Dreiecke, welche von geodätischen Linien auf Sphäroiden (abgeplatteten Rotationsellipsoiden) gebildet werden [6]–[8].
D. Loxodromische Trigonometrie heißt die Messung der Dreiecke, welche aus Loxodromenbögen auf der Kugel bestehen [9], [10].
Literatur: [1] Hammer, E., Lehrbuch der ebenen und sphärischen Trigonometrie, 2. Aufl., Stuttgart 1897. – [2] Heis und Eschweiler, Lehrbuch der Geometrie, 3. Teil, 7. Aufl., Cöln 1881. – [3] Reidt, Elemente der Mathematik, 4. Teil, 7. Aufl., Berlin 1891. – [4] Kambly, Die Elementarmathematik, für den Schulunterricht bearbeitet, III, Breslau 1895. – [5] Conradt, Lehrbuch der ebenen Trigonometrie, Leipzig 1889. – [6] Grunert, Sphäroidische Trigonometrie, Berlin 1833. – [7] Gudermann, Fundamenta trigonometriae sphaeroidicae exacta, Berlin 1847. – [8] Ciscato, Sulle formole fondamentali della trigonometria sferoidica, Venedig 1892. – [9] Grunert, Loxodromische Trigonometrie, Leipzig 1849. – [10] Gustavowicz, Theorie der loxodromischen Kurve und des loxodromischen Dreiecks mit Anwendung auf Kartographie und Auflösung nautischer Probleme, I und II, Krakau 1891/92. – [11] v. Braunmühl, Vorlesungen über Geschichte der Trigonometrie, I, Leipzig 1900. – [12] Killmann, P., Lehrbuch der ebenen Trigonometrie, 13. Aufl., Mittweida 1904. – [13] Lübsen, H.B., Ausführliches Lehrbuch der ebenen und sphärischen Trigonometrie, 19. Aufl., Leipzig 1908.
Wölffing.
http://www.zeno.org/Lueger-1904.