Differentialgetriebe

Differentialgetriebe ist ein Räderwerk, durch welches vermitteln zweier Drehungen eine dritte resultierende Drehung erzeugt wird, die der Differenz bezw. der Summe jener beiden Drehungen proportional ist.

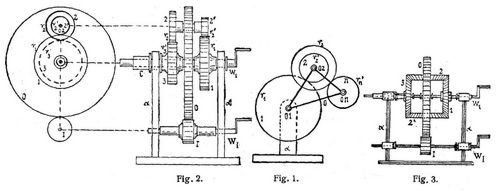
Mehrere der Reihe nach ineinander greifende Zahnräder 1, 2 ... n, deren Achsen 01, 02 ... 0n in einem Gliede 0, wie in Fig. 1, wo n = 3 ist, gelagert sind, bilden ein Vorgelege (s.d.). Bezeichnet r₁ den Radius des Teilkreises des Rades 1, ferner r₂, r'₂ die Radien der Teilkreise des Doppelrades 2–2' und r'_n den Radius des Teilkreises des letzten Rades n, und sind z₁, z₂, z'₂, z'_n die zugehörigen Zähnezahlen, so ist das Uebersetzungsverhältnis v vom Rade 1 zum Rade n oder das Verhältnis der Drehgeschwindigkeiten dieser beiden Räder, bestimmt durch

Dieses Verhältnis ist positiv oder negativ, je nachdem das erste Rad 1 und das letzte Rad n sich in gleichem oder entgegengesetztem Sinn drehen. Setzen wir dieses Vorgelege mit der Achse 01 drehbar auf ein festes Gestell α, dann erhalten wir ein nicht zwangläufiges Räderwerk. Drehen wir das Glied 0 im Gestell α mit der Drehgeschwindigkeit ω_0α und gleichzeitig das Rad 1 mit der Drehgeschwindigkeit ω_1α im Gestell α, dann wird durch diese zweifache Drehung das Räderwerk zwangläufig, d.h. es vollzieht eine bestimmte Bewegung, und in diesem Zustande wird dasselbe ein doppelwirkiges Umlaufgetriebe genannt [1]. Bezeichnet ω_nα die Drehgeschwindigkeit des Rades n in bezug auf das Gestell α, so ergibt sich für die Drehgeschwindigkeiten ω₁₀, ω_n0 der Räder 1, n in bezug auf das Glied 0, ω₁₀ = ω_1α – ω_0α, ω_n0 = ω_nα – ω_0α; und da das Verhältnis

ist, so folgt die fundamentale Beziehung:

aus der, wenn zwei von den drei Drehgeschwindigkeiten gegeben sind, die dritte berechnet werden kann. Wird dieses doppelwirkige Umlaufgetriebe nun so angeordnet, daß die Achse 0n des Rades n mit der im Gestell α gelagerten Achse 01 koinzidiert, dann drehen sich die Räder 1, n und das Glied 0 um die gemeinsame Achse 01 im Gestell α, und in dieser Gestaltung erhalten wir ein Differentialgetriebe oder Differentialräderwerk, weil die Drehgeschwindigkeit ω_1n des Rades 1 in bezug auf das koaxiale Rad n der Differenz der Drehgeschwindigkeiten ω_1α, ω_0α des Rades 1 und des Gliedes 0 proportional ist. Denn es ist: ω_1n = ω_1α – ω_nα, und demnach folgt aus der Gleichung 1.:

In der Praxis wird meistens die Anzahl der Räder n = 3 genommen, wie bei dem in Fig. 2 gezeichneten Differentialgetriebe, das im wesentlichen aus den beiden Rädern 1, 3 und dem[758] Doppelrade 2–2' besteht. Das Rad 1 ist auf der im Gestell α gelagerten Welle W₁ befestigt und das Rad 3 ist mit seiner Nabe c lose auf dieselbe gesetzt. Die Achse 02 des umlaufenden Doppelrades 2–2' ist in dem ebenfalls auf der Welle W₁ lose rotierenden Rad 0 gelagert, das jenes Glied 0 der Fig. 1 vertritt und von dem auf einer Welle W_I beteiligten, im Gestell α drehbaren Rade I getrieben wird. Wenn nun die Welle W₁ und die Welle W_I des Rades I gleichzeitig in Drehung versetzt werden, dann ist das Differentialgetriebe zwangläufig. Ist beispielsweise in Fig. 2 das Uebersetzungsverhältnis

dann ergibt sich aus 2. für die Drehgeschwindigkeit ω₁₃ des Rades 1 gegen das Rad 3, ω₁₃ = ¹/₂ (ω_1α – ω_0α). Werden die Räder 1 und 0 bezw. mit den Drehgeschwindigkeiten ω_1α, ω_0α in gleichen Sinne im Gestell α gedreht, so ist die Drehgeschwindigkeit ω₁₃ in diesem Falle gleich der halben Differenz der Drehgeschwindigkeiten der Räder 1 und 0. Drehen sich aber diese beiden Räder entgegengesetzt, dann ist die Drehgeschwindigkeit ω₁₃ gleich der der halben Summe ihrer Drehgeschwindigkeiten. – In Fig. 3 ist ein Differentialgetriebe mit Kegelrädern gezeichnet [2], Das Kegelrad 1 ist auf der im Gestell a gelagerten Welle W₁ fest, und auf dieser Welle ist das gleich große Kegelrad 3 sowie das Stirnrad 0 lose drehbar. In dem Stirnrade 0 ist die Achse des umlaufenden Kegelrades 2 radial gelagert, und wegen der Ausgleichung der Massen ist noch ein gleiches zweites Kegelrad 2' in derselben Weise eingesetzt. Die beiden umlaufenden Kegelräder 2, 2' greifen beiderseits in die Kegelräder 1, 3; und da diese gleich sind, so sind die Drehungen der Kegelräder 1, 3 in bezug auf das Stirnrad 0, das durch die Welle W_I vermitteln des Rades I getrieben wird, entgegengesetzt gleich. Es ist also das Uebersetzungsverhältnis v = – 1, und folglich ergibt sich aus 2. die Drehgeschwindigkeit ω₁₃ = 2 (ω_1α – ω_0α). Aus 1. erhalten wir in diesem Fall, wenn wir den Rädern 1, 3 entgegengesetzte Drehungen erteilen, also + ω_1α und – ω_3α einsetzen, ω_0α = ¹/₂ (ω_1α – ω_3α). Die Drehgeschwindigkeit des Rades 0 gegen das Gestell α ist hiernach gleich der halben Differenz der Drehgeschwindigkeiten der Räder 1, 3. In diesem Falle wird das Rad 0 ein Ditferentialrad genannt. Auf die mannigfaltigen Anwendungen der Differentialgetriebe in der Praxis wies Pecqueur[3] hin, und verschiedene Gestaltungen der Differentialgetriebe teilte Bock [4] mit.

Literatur: [1] Burmester, Lehrb. d. Kinematik, Leipzig 1888, Bd. 1, S. 503. – [2] Houldsworth Specification Nr. 5316 vom 16. Januar 1826; Polytechnisches Journal 1828, Bd. 30, S. 89. – [3] Pecqueur, Brevet 19 août 1824; Descriptions des machines t. 39, p. 66, und übersetzt in Demme, Der praktische Maschinenbauer 1842, 9. Liefg., S. 20. – [4] Bock, Ueber Differentialräderwerke, Zeitschr. d. Ver. deutsch. Ingen. 1879, Bd. 33, S. 411.

Burmester.

Fig. 1., Fig. 2., Fig. 3.