Pfeilzähne

Pfeilzähne hat Reuleaux die Radzähne benannt, welche nicht in gerader Linie, sondern im Winkel, wie stumpfe Pfeilspitze, auf dem Rade stehen (Fig. 1).

Wegen ihrer hervorragenden Bruchsicherheit werden sie für Betriebe mit großen Kräften und stoßender Gangart, trotz der Schwierigkeiten in der Herstellung, viel benutzt, besonders bei Walzwerken, schweren Blechscheren – und wegen ihres ruhigen Ganges auch für leichte Uebertragungen. Man läßt die Zähne mit den Spitzen vorangehen (Fig. 2). Es ist wichtig, darauf zu achten, daß die Schneide stumpf, die Kehle schärfer ausgebildet wird, weil im entgegengesetzten Falle die scharfe Schneide mit der stumpfen Kehle allein arbeiten würde, ohne daß die Flankenflächen der Zähne zur Berührung kämen. Beim Fräsen von Pfeilzähnen bleibt die Kehle rund und muß von Hand ausgearbeitet werden. Wenn man in Rücksicht hierauf die Zähne in der Mitte ausspart (s. Bd. 2, S. 628, Fig. 7 und 8., M N O) oder die Räder aus zwei Hälften je mit links und rechts geneigten Zähnen zusammensetzt, so verliert man die gegenseitige Versteifung der Zähne. Bei richtigem Gange berühren sich die Flanken in Linien, die schräg vom Fuß zum Kopf gehen. Es steht also nicht nur ein Punkt, sondern eine ganze Strecke der Zahnkurve, über die Radbreite verteilt, in Eingriff. Dadurch gleichen sich Unregelmäßigkeiten der Zahnform so weit aus, daß der Gang ruhiger wird. Dazu kommt noch, daß die Ablösung der zusammenarbeitenden Zahnpaare sanfter als sonst erfolgt, weil die Größe der Beführungsstrecke allmählich zu- und abnimmt. Als Voraussetzung für ruhigen Gang gilt, daß die Zähne jedes Rades und die Räder selbst mit einheitlicher Mittelebene gebaut und gelagert sind. Der Winkel 2 α (Fig. 1), welchen die beiden Schenkel eines Zahnes bilden, wird zu 110–130° angenommen, die Radbreite b = 4t, für mäßige Kräfte kleiner, für die stark beanspruchten Krauseln der Walzwerke aber größer. Der Sprung oder das Maß, um welches die Spitze des Zahnes den Enden vorausgeht, ergibt sich aus dem Winkel α und der Radbreite b zu ¹/₂b cotg α und kann größer, gleich oder kleiner als die Teilung t sein. Die Zahnhöhe h nimmt man zu 0,6 t mit 0,35 t für die Fußhöhe und 0,25 t für die Kopfhöhe. Als Zahnkurven eignen sich Evolventen, deren Eingriffslinie die Neigung von etwa 3 : 1 zur Zentralen hat (Fig. 2). Die Berührungsdruckkraft P : sin α ist für den winkelförmigen Zahn in demselben Maße größer wie die Flanke b : sin α länger als b ist. Die Abnutzung der Zahnflanke kann daher gleich der eines geraden Zahnes angenommen werden; in der Richtung des Umfanges fällt die Abnutzung größer aus. Durch die Winkelform ist der Zahn gegen Abbrechen gut gesichert. Die Zahnenden[95] sichert man für Betriebe mit starken Beanspruchungen und Stößen durch angegossene Randleisten, die fast bis zum Teilkreise reichen, und durch seitliche Abschrägung der Zahnköpfe (Fig. 1). Die Berechnung führt man, ohne Rücksicht auf die wirklichen, schwerlich festzustellenden Kräfte und Widerstandsmomente, in der für Zahnräder gebräuchlichen Weise durch und berechnet für die Umfangskraft von P kg die (im Umfang gemessene) Zahnstärke a 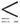0,5t aus der Biegungsformel ¹/₆a² b · s = P · h, wobei die Biegungsspannung s um so geringer anzusetzen ist, je stärkere Stöße zu erwarten sind, z.B. 400 kg/qcm für Gußstahl.

Das Rabitzgetriebe (von Joh. Renk in Augsburg) eignet sich für starke Uebersetzung von Elektromotoren, z.B. mit 3 und 30 Zähnen mit 2α = 40° oder mit 5 und 50 Zähnen mit 2α = 60°.

Literatur: Reuleaux, Der Konstrukteur, 4. Aufl., Braunschweig 1889; Bach, C., Maschinenelemente, 10. Aufl., Stuttgart 1908, S. 324 ff.; Oesterr. Zeitschr. für Berg- und Hüttenwesen 1890 S. 391; Zeitschr. d. Ver. deutsch. Ing. 1908, S. 661 ff.

Lindner.

Fig. 1.

Fig. 2.