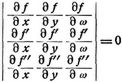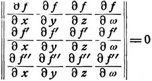- Jacobische Kurve
Jacobische Kurve. I. In der ebenen Geometrie hat die Jacobische Kurve der drei Kurven f (x y ω) = 0; f' = 0; f'' = 0 (wo ω homogenisierende Veränderliche) die Gleichung:
und ist der Ort eines Punktes, dessen Polargeraden in bezug auf die drei Kurven durch einen Punkt gehen.
Sie geht durch jeden gemeinsamen Punkt der drei Kurven und berührt daselbst, wenn zwei derselben von gleicher Ordnung sind, die dritte. Sind die Ordnungen aller drei Kurven gleich und ersetzt man die letzteren durch solche, welche dem durch sie bestimmten Kurvennetz (s. Kurven) angehören, so bleibt die Jacobische Kurve unverändert; sie gehört daher dem ganzen Netz zu. Besteht das Netz λ f + µ f' + γ f'' = 0 aus den Polaren sämtlicher Punkte der Ebene in bezug auf eine Kurve F = 0, so geht die Jacobische Kurve des Netzes in die Hessesche Kurve von F = 0 über [1]–[3].
II. In der Raumgeometrie hat die Jacobische Kurve von drei Flächen f(x, y, z, ω) = 0; f' = 0; f'' = 0 die Gleichungen:
und ist der Ort der Punkte, deren Polarebenen in bezug auf alle drei Flächen je durch eine Gerade gehen [4].
[223] Literatur: [1] Clebsch, A., Vorlesungen über Geometrie, herausgegeben von Lindemann, Bd. 1, Leipzig 1876, S. 377 ff. – [2] Salmon, G., Analytische Geometrie der Kegelschnitte, deutsch von Fiedler, 4. Aufl., Leipzig 1878, S. 551 ff. – [3] Ders., Analytische Geometrie der höheren ebenen Kurven, deutsch von Fiedler, 2. Aufl., Leipzig 1882, S. 194, 207. – [4] Ders., Analytische Geometrie des Raumes, deutsch von Fiedler, Bd. 1, 3. Aufl., Leipzig 1879, S. 316. – [5] Jacobi, Ueber die Funktionaldeterminanten, deutsch von Staeckel, Leipzig 1856.
Wölffing.
http://www.zeno.org/Lueger-1904.