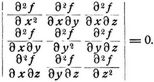Jacobische Kurve — Jacobische Kurve. I. In der ebenen Geometrie hat die Jacobische Kurve der drei Kurven f (x y ω) = 0; f = 0; f = 0 (wo ω homogenisierende Veränderliche) die Gleichung: und ist der Ort eines Punktes, dessen Polargeraden in bezug auf… … Lexikon der gesamten Technik
Kurven — Kurven, krumme Linien, stetige Reihen von Punkten in der Ebene. Eine solche wird durch eine Gleichung zwischen zwei Veränderlichen f (x, y) = 0 oder homogen f (x, y, ω) = 0, aufgelöst y = φ (x) dargestellt. Je nach der Natur der… … Lexikon der gesamten Technik
Determinanten — sind symbolische Ausdrücke für häufig vorkommende Eliminationsresultate, um die an sich schwerfälligen Ausdrücke in einfacher, übersichtlicher und für die Rechnung brauchbarer Gestalt schreiben zu können. Diese spielen in neuerer Zeit fast in… … Lexikon der gesamten Technik
Descartessches Blatt — (Folium von Descartes), eine Kurve dritter Ordnung. Gleichung x3 + y3 – 3pxy = 0, oder: Die Kurve besitzt die Wendeasymptote x + y + p = 0 und hat im Ursprung einen Doppelpunkt mit den Koordinatenachsen als Tangenten. – Hessesche Kurve… … Lexikon der gesamten Technik
Einheitsnormale — In der Geometrie ist ein Normalenvektor (auch: Normalvektor) ein Vektor, der senkrecht (orthogonal) auf einer Geraden, Kurve, Ebene, (gekrümmten) Fläche oder einer höherdimensionalen Verallgemeinerung eines solchen Objekts steht. Die Gerade, die… … Deutsch Wikipedia
Flächennormale — In der Geometrie ist ein Normalenvektor (auch: Normalvektor) ein Vektor, der senkrecht (orthogonal) auf einer Geraden, Kurve, Ebene, (gekrümmten) Fläche oder einer höherdimensionalen Verallgemeinerung eines solchen Objekts steht. Die Gerade, die… … Deutsch Wikipedia
Flächennormalenvektor — In der Geometrie ist ein Normalenvektor (auch: Normalvektor) ein Vektor, der senkrecht (orthogonal) auf einer Geraden, Kurve, Ebene, (gekrümmten) Fläche oder einer höherdimensionalen Verallgemeinerung eines solchen Objekts steht. Die Gerade, die… … Deutsch Wikipedia
Normale — In der Geometrie ist ein Normalenvektor (auch: Normalvektor) ein Vektor, der senkrecht (orthogonal) auf einer Geraden, Kurve, Ebene, (gekrümmten) Fläche oder einer höherdimensionalen Verallgemeinerung eines solchen Objekts steht. Die Gerade, die… … Deutsch Wikipedia
Normaleneinheitsvektor — In der Geometrie ist ein Normalenvektor (auch: Normalvektor) ein Vektor, der senkrecht (orthogonal) auf einer Geraden, Kurve, Ebene, (gekrümmten) Fläche oder einer höherdimensionalen Verallgemeinerung eines solchen Objekts steht. Die Gerade, die… … Deutsch Wikipedia
Normalkomponente — In der Geometrie ist ein Normalenvektor (auch: Normalvektor) ein Vektor, der senkrecht (orthogonal) auf einer Geraden, Kurve, Ebene, (gekrümmten) Fläche oder einer höherdimensionalen Verallgemeinerung eines solchen Objekts steht. Die Gerade, die… … Deutsch Wikipedia