Katakaustik, katakaustische Fläche

Katakaustik, katakaustische Fläche. In derselben Weise, wie die diakaustische Fläche (s. Diakaustik, S. 165) durch Brechung der Lichtstrahlen an einer Fläche oder einer Folge von Flächen, die Diakaustik durch den ebenen Achsenschnitt der diakaustischen Fläche[405] entsteht, so entsteht die katakaustische Fläche durch Reflexion der Strahlen an einem krummflächigen Spiegel oder einer Folge solcher Spiegel, die Katakaustik durch den ebenen Achsenschnitt der Fläche. Alles was bei der Diakaustik über die in der Achse liegenden Spitzen, das Bild eines leuchtenden Punktes, die Hauptfläche, die Hauptpunkte, die Brennpunkte, die Brennweite, die Hauptebene gesagt wurde, gilt auch für die Katakaustik. – Von besonderem Interesse ist die durch Spiegelung der Lichtstrahlen an einem Kreise entstehende Katakaustik. Liegt der leuchtende Punkt L im Unendlichen, so ist die Katakaustik eine Epizykloide, die durch das Rollen eines Kreises vom Radius r/4 auf einem Kreise vom Radius r/2, wenn r der Radius des spiegelnden Kreises ist, entsteht. Die beiden Spitzen liegen auf der Achse zu beiden Seiten des Mittelpunkts im Abstande r/2 von ihm. Liegt L in der Entfernung a von dem Mittelpunkte außerhalb des Kreises, so liegen die Spitzen zu beiden Seiten des Mittelpunkts auf der Achse in den Abständen a r/(2a – r) und a r/(2a + r) vom Mittelpunkte; die Kurve berührt den Kreis in denselben Punkten, in denen er von den von L ausgehenden Tangenten berührt wird.

Liegt L auf dem Kreise, so geht die Kurve in eine Epizykloide (Kardioide) über, die durch das Rollen eines Kreises vom Radius r/3 einem festen Kreise von demselben Radius entsteht; die Kurve berührt jetzt den Kreis in L, und die eine noch vorhandene Spitze liegt auf der Achse im Abstande r/3 vom Mittelpunkte. – Liegt L innerhalb des Kreises und ist a > r/2, so zerfällt die Kurve in zwei getrennte Aeste, die zwei sich in der Achse schneidende und mit ihr gleiche Winkel bildende Asymptoten besitzen. Außer den beiden in der Achse liegenden Spitzen treten noch zwei außerhalb der Achse symmetrisch gegen sie liegende Spitzen auf.

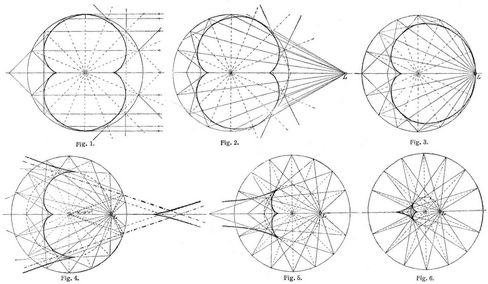
[406] Ist a = r/2, so fallen die beiden Asymptoten mit der Achse zusammen. Die eine auf der Achse liegende Spitze hat vorn Mittelpunkte den Abstand r/4, während die andre in unendlicher Ferne liegt. Die beiden Nebenspitzen bleiben bestehen. Ist endlich a < r/2, so schrumpft die Katakaustik zu einem krummlinigen Viereck mit zwei auf der Achse und zwei außerhalb der Achse liegenden Spitzen zusammen. In den drei letzten Fällen liegen die beiden Nebenspitzen auf einem um den Mittelpunkt des Kreises mit dem Radius a beschriebenen Kreise, der in ihnen die Kurve berührt. – Die Fig. 1–6 zeigen die Gestalten der Katakaustik für a = ∞, a = 2r, a = r, a = ³/₄r, a = ¹/₂r, a = ¹/₄r. Bei ebenen Spiegeln ergibt sich keine Katakaustik, weil die gespiegelten Strahlen genau wieder durch einen Punkt gehen.

Literatur: Meisel, Geometr. Optik, Halle 1886.

F. Meisel.

Fig. 1., Fig. 2., Fig. 3., Fig. 4., Fig. 5., Fig. 6.