- Kreis
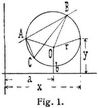
Kreis, eine Kurve, deren sämtliche Punkte von einem Punkte, dem Mittelpunkt oder Zentrum, gleichen Abstand haben. Die Verbindung eines Kreispunkts mit dem Mittelpunkt heißt Radius (Halbmesser). Die Gleichung eines Kreises (Fig. 1) vom Mittelpunkt a, b und Radius r ist (x – a)2 – (y – b)2 = r2.
Ein Kreis ist durch drei seiner Punkte (x1 y1); (x2 y2); (x3 y3) bestimmt; seine Gleichung ist:
Die Kreisgleichung hat als quadratische Glieder x2 + y2; alle Kreise schneiden die unendlich ferne Gerade in den imaginären Kreispunkten
Die Verbindungsgerade zweier Kreispunkte heißt Sehne, und wenn sie durch den Mittelpunkt geht, Durchmesser. Jeder Durchmesser wird im Mittelpunkt halbiert. Ein Stück der Kreislinie heißt Bogen; ein Stück der Kreisfläche, das von einer Sehne und einem Bogen begrenzt ist, Segment (Abschnitt). Jeder Durchmesser teilt den Kreis in zwei Halbkreise. Ist (Fig. l) A B eine Sehne, O der Mittelpunkt, so heißt A O B Zentriwinkel. Die von A O, B O und Bogen A B begrenzte Fläche heißt Sektor (Ausschnitt); speziell Quadrant, Sextant, Oktant, wenn der Zentriwinkel 90°, 60°, 45° beträgt. Eine den Kreis schneidende Gerade heißt Sekante und, wenn sie durch den Mittelpunkt geht, Zentrale.
Zwei Kreise heißen konzentrisch, wenn sie denselben Mittelpunkt haben, sie berühren sich in den unendlich fernen Kreispunkten, ihre Gleichungen unterscheiden sich nur im Absolutglied.
Das Lot vom Mittelpunkt auf die Sehne halbiert diese, den Zentriwinkel und den Bogen. Zwei gleiche Sehnen haben vom Mittelpunkt gleichen Abstand. Ist C ein weiterer Kreispunkt, so ist der Peripheriewinkel A C B gleich der Hälfte des Zentriwinkels A O B. Alle Peripheriewinkel in demselben Bogen sind gleich (Satz des Thales: Der Peripheriewinkel im Halbkreis ist ein rechter). Die Tangente steht auf dem Radius in seinem Endpunkt senkrecht. Von einem Punkt außerhalb gehen an einen Kreis zwei Tangenten, deren Länge bis zum Berührungspunkt gleich ist;, die Zentrale des Punktes halbiert ihren Winkel. Der Winkel zwischen einer Sehne und der Tangente in einem ihrer Endpunkte (Tangentensehnenwinkel) ist gleich dem zugehörigen Peripheriewinkel. Zwei Kreise schneiden sich entweder in zwei reellen oder in zwei imaginären Punkten, oder sie berühren sich in einem Punkt der gemeinsamen Zentrale.
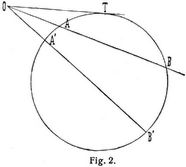
Zwei Kreise besitzen vier gemeinsame Tangenten; bei den beiden äußeren liegen die Kreise auf derselben, bei den inneren auf verschiedenen Seiten der Tangente. Die Abschnitte der äußeren Tangenten zwischen den Berührungspunkten sind einander gleich und gleich den Abschnitten der inneren zwischen den äußeren. Gehen durch einen Punkt O mehrere Sekanten, O A B, O A' B' (Fig. 2), so ist das Produkt der Abschnitte jeder derselben von O bis zum Kreis konstant. Dasselbe heißt Potenz von O in bezug auf den Kreis und ist gleich dem Quadrat der Tangente von O an den Kreis. Das Tangentenpaar des Punktes (x1 y1) an den Kreis x2 + y2 – r2 = 0 hat die Gleichung: (x12 + y12 – r2)(x2 + y2 – r2) – (x x1 + y y1 – r2)2 = 0. Die Gerade x x1 + y y1 – r = 0 ist die Berührungssehne (Polare) des Punkts x1 y1 in bezug auf den Kreis, und dieser Punkt ist ihr Pol. Die Polaren aller Punkte einer Geraden gehen durch den Pol, die Pole aller Geraden durch einen Punkt liegen auf dessen Polare. Der Inhalt der Kreisfläche ist r2 π, wo π die Ludolfsche Zahl 3,1415926 ...; der Inhalt eines Sektors vom Zentriwinkel α0 ist r2 π α/360, der Inhalt des zugehörigen Segments ist r2 π α/360 – 1/2 r2 cos α. Die Länge der Kreisperipherie ist 2r π, die Länge des Bogens vom Zentriwinkel α0 r π α/180. Die Punkte der Zentrale, in welchen sich die inneren/äußeren gemeinsamen Tangenten scheiden, heißen inneren/äußeren Aehnlichkeitspunkt (Kontingenzpunkt). Die Verbindungslinie der Endpunkte zweier parallelen Halbmesser geht durch den äußeren/inneren Aehnlichkeitspunkt, je nachdem die Halbmesser gleich/entgegengesetzt gerichtet sind. Auf jeder Linie durch einen Aehnlichkeitspunkt (Aehnlichkeitslinie) werden durch die beiden Kreise vier Abschnitte (vom Aehnlichkeitszentrum aus gemessen) bestimmt. Das Produkt der beiden äußeren und das Produkt der beiden inneren ist je von der Wahl der Aehnlichkeitslinie unabhängig. Satz von Monge: Sind drei Kreise gegeben, so liegen von den Aehnlichkeitspunkten,[686] die sie paarweise bestimmen, die drei äußeren, ebenso je zwei innere mit dem nicht zugehörigen äußeren in gerader Linie: vier Aehnlichkeitsachsen. Der Ort eines Punktes, welcher in bezug auf zwei Kreise dieselbe Potenz (s. oben) besitzt, ist eine Gerade, die Chordale oder Radikalachse der Kreise, sie geht durch die Schnittpunkte der Kreise. Sind daher K = 0 und K' = 0 zwei Kreise, so hat das Kreisbüschel K + λ K' = 0 eine gemeinsame Radikalachse. In dem Büschel existieren zwei Kreise, welche sich auf einen Punkt reduzieren: die sogenannten Grenzpunkte des Büschels. Die Punkte liegen auf der gemeinsamen Zentrale, und jeder hat das im andern auf der Zentrale errichtete Lot zur Polare in bezug auf jeden der Kreise des Büschels. Zieht man von einem Punkt der Radikalachse an alle Büschelkreise Tangenten, so ist der Ort der Berührungspunkte ein Kreis, der alle Büschelkreise unter rechtem Winkel schneidet und durch die Grenzpunkte geht (Orthogonalkreis). Für drei Kreise, welche nicht einem Büschel angehören, gibt es wenigstens einen Orthogonalkreis. Sein Mittelpunkt ist das Radikalzentrum (Chordalpunkt), in welchem sich die Radikalachsen der einzelnen Kreispaare schneiden. Es existieren acht Kreise, welche je drei gegebene berühren (Taktionsproblem des Apollonius).
Literatur: [1] Salmon, Analytische Geometrie der Kegelschnitte, deutsch von Fiedler, 5. Aufl., Bd. 1, Leipzig 1887, Kap. 7–10. – [2] Fiedler, W., Cyclographie, Leipzig 1882. – [3] Mac Clelland, W.D., Geometry of the Circle, London 1891. – [4] Mack, L., Analytische Geometrie des Kreises, Stuttgart 1855; s. ferner Literatur unter Geometrie [1]–[5].
Wölffing.
http://www.zeno.org/Lueger-1904.