Astatik

Astatik, ein besonderer Zweig der Lehre von der Ersetzung der Kräfte an einem starren Körper (s. Aequivalenz der Kräfte). Derselbe entstand im Verfolg der Frage nach dem Vorhandensein eines »Mittelpunktes« der angreifenden Kräfte. Im Falle paralleler Kräfte ist ein solcher Mittelpunkt im Schwerpunkt der Angriffspunkte, die man sich mit Maßen proportional den wirkenden Kräften belegt denkt, immer vorhanden. Ist dieser Schwerpunkt unterstützt, so ist der Körper unter dem Einfluß der Parallelkräfte in jeder Lage im Gleichgewicht, und dieses heißt ein astatisches. Unter dem Namen Astatik faßt man nun alle Untersuchungen zusammen, die sich auf den Fortbestand der Wirkung eines an einem starren Körper angreifenden Kräftesystems beziehen, wobei die Angriffspunkte der Kräfte im Körper fest bleiben und die Kräfte selbst ihre Richtung und Größe beibehalten, während die Lage des Körpers gegen das Kräftesystem sich ändert.

Parallelverschiebung des Körpers ändert die Wirkung der Kräfte auf den Körper nicht, nur Drehung. Die astatische Wirkung eines Kräftesystems P_i mit den Komponenten X_i, Y_i, Z_i, die in den Punkten mit den Koordinaten X_i, Y_i, Z_i angreifen, ist durch folgende 12 Größen bestimmt:

Sind dieselben gleich null, so ist der Körper im asiatischen Gleichgewicht, d.h. in einem Gleichgewicht, das auch dann noch aufrechterhalten bleibt, wenn man den Körper dreht, während die Kräfte an ihren Angriffspunkten in gleicher Richtung und Größe wirken. Für das gewöhnliche Gleichgewicht, wobei die Kräfte in ihren Wirkungslinien verschiebbar gedacht sind, müssen nur sechs Bedingungen erfüllt sein, nämlich

A = B = C = 0 und a₁₂ – a₂₁ = a₂₃ – a₂₃ = a₃₁ – a₁₃ = 0.

Die zwölf Bedingungen des asiatischen Gleichgewichtes ergeben sich, wenn man ausdrückt, daß nach Drehung des Körpers um jede der drei Koordinatenachsen unabhängig vom Drehwinkel φ noch gewöhnliches Gleichgewicht zwischen den angreifenden Kräften herrscht.

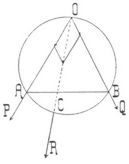
Die eingangs erwähnte Frage nach dem Vorhandensein eines asiatischen Mittelpunktes, durch den die Resultante des Kräftesystems in jeder Lage des Körpers hindurchgeht, ist außer für Parallelkräfte auch noch für Kräfte in einer Ebene allgemein zu bejahen. Betrachten wir zunächst zwei Kräfte P und Q (s. die Figur) in der Ebene, die in den Punkten A und B angreifen und kein Paar bilden. Dreht man beide, ohne ihre gegenseitige Neigung zu ändern, um ihre Angriffspunkte, so beschreibt der Schnittpunkt O ihrer Richtungslinien einen durch AB gehenden Kreis. Auf diesem liegt der astatische Mittelpunkt der Kräfte und zwar im Punkt C, in dem die durch O gehende Resultante der Kräfte P und Q den Kreis schneidet. Werden die Kräfte parallel, so geht der Kreis in die Gerade AB über und C wird der Drehpunkt des Hebels, an dem sich die Kräfte das Gleichgewicht halten. Um für mehr als zwei Kräfte in der Ebene den asiatischen Mittelpunkt zu finden, zerlegt man alle Kräfte in die Komponenten X und Y, sucht den Mittelpunkt A des X-Komponenten und jenen B des Y-Komponenten. Der astatische Mittelpunkt des Systems ist dann der Mittelpunkt C der beiden Kräfte ΣX und ΣY, die in A und B angreifen.

Befindet sich ein räumliches System, das um eine feste Achse drehbar ist, im nichtastatischen Gleichgewicht, so kann man die zur Achse senkrechten (und daher einer Ebene parallelen) Komponenten der Kräfte durch ihre astatische Resultante ersetzen, ohne daß die Art des Gleichgewichts (ob stabil oder labil) geändert wird.

Ein freies räumliches Kräftesystem, das nicht im asiatischen Gleichgewicht ist, hat nur ausnahmsweise einen asiatischen Mittelpunkt. Man findet die Bedingungen des Vorhandenseins eines solchen sowie dessen Koordinaten, indem man an dem noch unbekannten Punkt die Resultante der wirkenden Kräfte in entgegengesetzter Richtung anbringt und die Bedingungen des astatischen Gleichgewichtes des so ergänzten Kräftesystems ausdrückt.

Literatur: Schell, Theorie der Bewegung und der Kräfte, 2. Aufl., Bd. 2, Kap. XI, Leipzig 1879,80. – Darboux, Memoire sur l'équilibre astatique, Paris 1877.

S. Finsterwalder.