Spiegel- und Prismeninstrumente

Spiegel- und Prismeninstrumente oder allgemein Reflexionsinstrumente dienen zur Messung von Winkeln, indem man von den Prinzipien der Reflexion des Lichtes an Spiegelflächen oder der totalen Reflexion in Prismen Gebrauch macht.

Die Veränderung der Stellung der reflektierenden Flächen zueinander wird mittels Kreisbogens meßbar gemacht. Diese Instrumente haben den Vorteil, daß sie keiner seiten Aufstellung bedürfen und man mit ihnen in der Lage ist, Winkel in beliebigen Ebenen zu messen. Sie eignen sich daher vornehmlich zu Messungen auf See, wo feste Aufstellung unmöglich ist. Die Reflexionsinstrumente können so eingerichtet sein, daß man mit ihnen Winkel beliebiger Größe (0–180°) messen kann (Oktant, Sextant, Prismen- oder Spiegelkreis) oder daß sie nur, wie es in der niederen Geodäsie häufig und an Bord in einzelnen Fällen vorkommt, zur Absteckung oder zum Einvisieren in Winkel von 45°, 90° oder genau zwischen zwei Punkte (Winkel von 180°) eingerichtet sind (Winkelspiegel, Prismenkreuz u.s.w.). Die Reflexionsinstrumente der ersteren Art können in der astronomischen Navigation und zu astronomischen Zeit- und Ortsbestimmungen an Land, in letzterem Falle mit Benutzung eines sogenannten künstlichen Horizontes (s.d.) gebraucht werden.

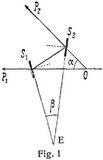
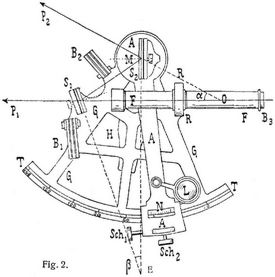
Die Erfindung der Spiegelsextanten (als den am weitesten verbreiteten Vertreter dieser Gattung von Instrumenten hier als typisch angeführt) wird dem Engländer Hadley zugeschrieben, der 1742 der Royal Society in London eine Beschreibung und ein solches Instrument (einen Oktanten) vorlegte [1]. Tatsächlich scheint auch Newton schon 50 Jahre früher auf eine ähnliche Idee gekommen zu sein, denn er hatte, wie sich nach dem Tode von Hadley herausstellte, diesem schon 1699 eine Skizze zu einem Spiegelinstrument eingereicht, welche aber in Vergessenheit geraten war, da seine Angaben ein zu unförmliches Instrument bedingt hätten (Ueber nähere Angaben betreffend die Erfindungsgeschichte ist zu vergleichen Wolf, Handbuch der Astronomie II, S. 53–56). Die Theorie der Reflexionsinstrumente, welche für alle Formen im wesentlichen dieselbe bleibt, mag nachstehend am Sextanten erläutert werden. In Fig. 1 u. 2 sind S₁ und S₂ zwei Spiegel, von denen S₂ (großer Spiegel) mit seiner reflektierenden Fläche im Zentrum des Kreissektors T M T um eine zu diesem senkrechte Achse beweglich[184] angebracht und mit seiner spiegelnden Fläche nach links gerichtet ist; fest mit ihm verbunden und daher gleichzeitig mit um dieselbe Achse beweglich ist die Alhidade A. Der Spiegel S₁ (kleiner, fester Spiegel) ist auf dem Sektor selbst befestigt und kann zur Ebene des Sextanten vermitteln entsprechender Schrauben senkrecht gestellt werden. Die obere Hälfte dieses Spiegels ist unbelegt, während die untere nach der Seite des Fernrohres F hin als Spiegel wirkt. Befindet sich nun z.B. in der Richtung nach P₁ ein Objekt, so wird man dieses im Fernrohr durch den unbelegten Teil des Spiegels S₁ hindurch wahrnehmen können. Licht, welches aus der Richtung von P₂ kommt, wird bei der skizzierten Stellung des Spiegels S₂ an diesem reflektiert nach S₁ gelangen und von da gleichfalls in das Fernrohr reflektiert werden. Man wird also in diesem gleichzeitig ein Bild von P₁ und von P₂ wahrnehmen und beide Bilder werden durch geeignete Stellung von S₂ und damit der Alhidade A zur Deckung gebracht werden können unter der Voraussetzung, daß die Ebenen der beiden Spiegel senkrecht zur Sextantenfläche und parallel zur Umdrehungsachse des Spiegels S₂ und der Alhidade stehen. Ist die Koinzidenz der Bilder, von denen jedes mit Benutzung der entsprechenden Hälfte des Fernrohrobjektivs zustande kommt, hergestellt, so ist leicht einzusehen, daß die Drehung des großen Spiegels von einer bestimmten Lage, der Nullstellung, aus ein Maß für die Größe des Winkels sein wird, unter dem sich die beiden Visierlinien nach P₁ und P₂ am Orte des Beobachters schneiden. Die Nullstellung wird auf der Teilung da anzusetzen sein, wo der Nullpunkt der Ablesevorrichtung (Vernier) steht, wenn die beiden Spiegelflächen parallel, also die Richtungen nach P₁ und P₂ ebenfalls parallel sind, d.h. im Fernrohr derselbe sehr weit entfernte Gegenstand am gleichen Orte des Gesichtsfeldes abgebildet wird. Die Beziehungen zwischen den einzelnen Richtungen sind dann folgende, wenn man setzt ∢ O S₁ S₂ = 2δ und ∢ S₁ S₂ P₂ = 2γ:

Aus Dreieck O S₁ S₂ : α + 2δ + (180° – 2γ) = 180°; α = 2γ – 2δ,

Aus Dreieck S₁ S₂ E : β + (90° + δ) + (90° – γ) = 180°; β = γ – δ = α/2.

Danach ist also der Drehungswinkel des Spiegels S₂ von seiner Nullstellung aus gleich der Hälfte desjenigen Winkels, unter dem die Objekte in P₁ und P₂ vom Beobachter aus erscheinen. – Ist daher die Teilung auf dem Limbus des Instruments so eingerichtet, daß man an ihm bei Bezifferung des betreffenden Bogens mit seinem doppelten Winkelwert sofort die Drehung der Alhidade A ablesen kann, so kann der Winkel α mit einem solchen Instrumente bestimmt werden, falls die Nullangabe des Limbus mit der Parallelstellung der beiden Spiegel zusammenfällt. Ist das nicht der Fall, so muß eben derjenige Punkt auf der Teilung bestimmt werden, der der Parallelstellung von S₁ und S₂ entspricht; die Differenz gegen Null nennt man die Indexkorrektion, sie muß der Ablesung hinzugefügt werden, wenn man bei Parallelität der beiden Spiegel, also bei Koinzidenz der beiden Bilder eines sehr entfernten Objektes, an der Teilung eine Stelle abliest, die von der Null aus nach rechts, also außerhalb der Teilung von 0 bis 120°, liegt. Abzuziehen ist die Korrektion, wenn man bei der erwähnten Stellung der Spiegel eine Angabe am Instrument abliest, die links der Null, also innerhalb der eigentlichen Teilung liegt. Um im ersteren Fall ablesen zu können, sind die Teilungen auf derartigen Instrumenten immer noch um einige Grade über Null hinaus fortgesetzt, also dahin, wo dann 359°, 358° u.s.w. zu stehen kommen würde. – Bei den später zu besprechenden Vollkreisen hat man auch die Einrichtung getroffen, daß man die Teilung zu beiden Seiten der Null fortgesetzt hat. Benutzt man dann das Instrument einmal mit Teilung nach unten (rechts) und dann zu einer zweiten Messung mit Teilung nach oben (links), so wird aus dem Mittel beider Resultate der Indexfehler eliminiert. Das Verfahren läßt sich aber nur bei besonders dazu eingerichteten Instrumenten anwenden, ist aber sehr empfehlenswert z.B. bei Messung genauer Monddistanzen. – Das Fernrohr hat wegen der Anwendung des Instruments in freier Hand nur eine geringe Vergrößerung (4–10 fach), daher ein großes Gesichtsfeld; eine Markierung der Mitte des Gesichtsfeldes ist nur dadurch herbeigeführt, daß aus vier starken Drähten ein Quadrat von etwa ¹/₂–1° Seitenlänge gebildet wird, in dessen Raum die Koinzidenzen zu bewerkstelligen sind. Eine Abweichung von dieser Regel in zur Sextantenebene senkrechtem Sinne würde gleichbedeutend sein mit einer stärkeren Neigung des Fernrohres gegen diese Fläche, was in jedem Fall den gemessenen Winkel zu groß erscheinen lassen würde [2]. – Da man sowohl bei irdischen Objekten als auch bei astronomischen – Sonne und Mond, Mond und Sterne – Bilder von zu großer oder sehr verschiedener Helligkeit erhalten würde, sind verschiedene Blendeinrichtungen vorgesehen. Einmal kann für Sonnenbeobachtungen vor das Okular ein Blendglas gesetzt werden, welches beide Lichtbüschel natürlich in gleicher Weise abblendet und dadurch die Messung von Fehlern, die durch die beiden Blendeinrichtungen bei B₁ und B₂ die aus zwei oder mehr farbigen Gläsern bestehen, wegen nicht bestehender Planparallelität der Gläserflächen bedingt werden, frei macht. – Um außerdem noch Ausgleich der Helligkeiten der Bilder herbeizuführen, ist das Fernrohr bei R in einen Ring eingeschraubt, der durch eine zur Sextantenebene senkrechte Führung und Schraube der ersteren genähert und von ihr entfernt werden kann, wodurch bald ein größerer Teil des Objektivs von dem doppelt reflektierten Bilde, bald von dem direkt gesehenen ausgenutzt wird. Der Ring R gestattet auch zugleich durch geeignet angebrachte Korrektionsschrauben eine Veränderung der Neigung des Fernrohres zur Sextantenebene (s. oben). Da die Mitte des großen Spiegels S₁ nicht in die Visur nach dem Objekte P₁ fällt, wird für nähere Objekte der Indexfehler anders sein als für sehr entfernte oder cölestische, denn der Abstand des Spiegels S₂ von der Linie P₁O kann dann nicht vernachlässigt werden, man nennt das die Parallaxe des Sextanten. – Fällt die Umdrehungsachse der Alhidade A nicht mit dem Teilungszentrum zusammen, so wird die Ablesung am Limbus einen sogenannten Exzentrizitätsfehler besitzen, den schlimmsten Fehler der Sextanten und Oktanten. Eine Bestimmung dieses Fehlers ist in der Praxis nur möglich durch Vergleichung der Angaben des zu prüfenden Instruments mit einer Anzahl von genau bekannten Winkeln möglichst verschiedener Größe. Zwei solcher Vergleichungen würden theoretisch schon[185] genügen, man macht aber meist viel mehr (6–10). Die seefahrenden Nationen besitzen besondere Institute (Deutschland die Deutsche Seewarte in Hamburg), in denen die Prüfungen der Reflexionsinstrumente systematisch vorgenommen werden [3]. Auf besonderen Attesten werden die Fehlertabellen dann den Käufern übermittelt. Wichtige und umfangreiche Erfahrungen sind auf diese Weise über die zweckmäßige Einrichtung, und Beschaffenheit solcher Instrumente gewonnen worden [3], [4]. Wegen der verschiedenen Arten von Oktanten und Sextanten, die man im Laufe der Jahre gebaut hat, um bald die eine oder andre Verbesserung oder einen bequemeren Gebrauch (Dosensextanten) zu erzielen, muß hier auf die Literatur, besonders auf [5] verwiesen werden. Dahin gehören auch die Konstruktionen zur Ausschaltung der Kimm als Horizont und zur Vermeidung der Fehler, die durch unrichtige Annahmen über Kimmtiefe bedingt werden. Dazu ist besonders zu vergleichen die Beschreibung der Apparate von Reitz, Fleurais [8] und in neuerer Zeit von Pulfrich und Kohlschütter [12]. Um den schlimmsten Fehler des Sextanten (s. oben), die Exzentrizität, unschädlich zu machen, ist man schon im 18. Jahrhundert dazu übergegangen, Vollkreise an die Stelle der Sektoren zu setzen, so daß die Teilung an zwei diametral stehenden Verniers abgelesen werden kann, wodurch bekanntlich der Exzentrizitätsfehler fast vollständig eliminiert werden kann [6]. Tob. Mayer (1752) und Borda (1787) bauten solche Instrumente, welche außerdem so eingerichtet waren, daß man an ihnen das Verfahren der sogenannten Repetition der Winkelmessung ausführen konnte. Es wurde das durch meßbares Verstellen des Spiegels S₁, der dann etwas anders angeordnet war, bewirkt. Diese Konstruktionen (vgl. [7]) haben sich nicht bewährt und sind nur seiten in Gebrauch gekommen, dagegen hat die Form, welche Pistor & Martins 1845 den Vollkreisen gegeben haben [11], weite Verbreitung gefunden. Sie setzten zugleich an die Stelle des »kleinen« Spiegels S₁ ein totalreflektierendes, gleichschenkeliges Prisma [8]. Die Reflexion findet dann an der Grundfläche desselben in der in Fig. 3 angedeuteten Weile statt. Diese »Prismenkreise« haben den Vorzug, daß mit ihnen Winkel bis 180° gemessen werden können, daß die Beschaffenheit der Bilder namentlich bei großen Winkeln viel besser ist als bei den Sextanten (dafür ist bei sehr kleinen Winkeln allerdings das Umgekehrte in gewissem Maße der Fall) und daß endlich der Exzentrizitätsfehler wegfällt, wie oben schon. gesagt. – Nach Pistor & Martins haben namentlich Wegener und besonders Wanschaff in Berlin, dann auch Hamburger Mechaniker, die im übrigen sehr gute Sextanten liefern (Plath, Hechelmann), solche Prismenkreise gebaut. Leider ist ihre Einführung in den Seefahrtskreisen noch immer nicht in genügender Weise gefördert, da der Seemann nur schwer von dem alten Gebrauch des Sextanten, an dem er besonders den größeren Kreisdurchmesser bei gleicher Handlichkeit des Instruments schätzt, abzubringen ist. Es unterliegt keinem Zweifel, daß die Vollkreise, mögen sie nun die Prismenreflexion oder den Spiegel (Spiegelkreise) benutzen, ganz erhebliche Vorzüge besitzen. – Besonders der Umstand, daß bei allen diesen Instrumenten die sogenannte Parallaxe (s. oben) noch einen Mangel bedeutet, da der Indexfehler dadurch für verschieden entfernte Objekte sich ändert, hat dazu geführt, daß man auch Reflexionsinstrumente gebaut hat, bei denen die beiden reflektierenden Flächen zur Achse des Instruments konzentrisch liegen (solche Instrumente sind noch vor Pistor & Martins, von Steinheil und später auch von Wegener gebaut worden [9]). Zwei übereinander liegende, total reflektierende Prismen (bei Steinheil rechtwinklige, bei Wegener nur gleichschenkelige) bewirken die Visur nach den beiden Objekten. Ihr Drehungswinkel – Winkel zwischen den reflektierenden Flächen – ist dann gleich dem halben Winkel zwischen den beiden Objekten. Diese Instrumente eignen sich auch bei Gebrauch auf Stativ gut für terrestrische (horizontale) Messungen. Betreffs Konstruktion dieser Instrumente muß auch auf die Werke [8] verwiesen werden. – Mit einiger Verkennung der Leistungsfähigkeit der genannten Reflexionsinstrumente hat man auch solche [10] gebaut, bei denen die Kreisablesung mittels Schraubenmikroskope ausgeführt wird. Solche Instrumente sind höchstens bei Benutzung sehr sicherer Stative mit Vorteil zu gebrauchen. Im allgemeinen ist der Gebrauch von Stativen eher unbequem, als der Beobachtung förderlich, mit Ausnahme vielleicht bei Messungen von Monddistanzen (s.d.).

Literatur: [1] Philosoph. Transact. 1731, S. 147, und 1732, S. 341. – [2] Encke, Ueber den Spiegelsextanten, Berl. Astron. Jahrbuch 1830, S. 292 (Gesammelte Abhandl., herausgegeben von Gravelius); Bohnenberger, Anleitung zur geogr. Ortsbestimmung u.s.w., Göttingen 1795. – [3] Eylert, Der Sextant, Aus dem Archiv der Deutschen Seewarte, 1881, Nr. 4. – [4] Annalen der Hydrographie, 6. Jahrg., S. 380 ff. – [5] Jordan, Grundzüge der astron. Zeit- und Ortsbestimmungen, Berlin 1885, S. 154 ff.; Ambronn, L., Handbuch der astron. Instrumentenkunde, 1898, II, S. 796 ff. – [6] Bezüglich der Bestimmung der Exzentrizität vgl. Jordan, ebend., Ambronn, L., II, S. 790 ff., und die Handbücher der sphär. Astronomie. – [7] Ambronn, L., II, S. 798 ff. – [8] Hunaeus, Jordan, Ambronn, in den angegebenen Werken. – [9] Hunaeus, Praktische Geometrie, Hannover 1868, S. 153 ff. – [10] Ambronn, L., II, S. 810. – [11] Berliner Gewerbe-, Industrie- und Handelsblatt 1845, Bd. 14, S. 17 ff. – [12] Annalen der Hydrographie, 1903, 31. Jahrg., S. 533 ff.; Zeitschr. f. Instrumentenkunde 1904, 24. Jahrg., S. 225 ff. – Im übrigen mag noch auf die folgenden Werke, welche neben vielen andern über den Gebrauch der Reflexionsinstrumente und ihre Korrektur u.s.w. handeln, hingewiesen werden: Bessel (Untersuchung der Sextanten betreffend), Abhandlungen, Bd. 2, S. 166 ff., Wislicenus, Handbuch der geographischen Ortsbestimmungen, Leipzig 1891. – Caspari, Astronomie pratique, Paris 1888, Bd. 1, S. 187 ff., ziemlich ausführliche Theorie; Handbuch der Navigation und Handbuch der nautischen Instrumente, beide herausgegeben vom Reichsmarineamt.

Ambronn.

Fig. 1.

Fig. 2.

Fig. 3.