Stufenscheibe

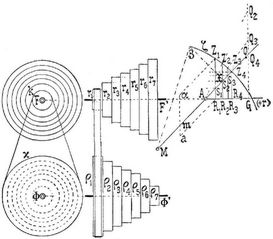
Stufenscheibe. Soll die Uebertragung der Drehung in der Figur von einem Scheibenkörper Φκ, auf einen andern Scheibenkörper F k, welche sich beide um parallele Achsen F, Φ drehen, vermitteln eines nicht gekreuzten Treibriemens von unveränderlicher Länge in verschiedenen gegebenen Umdrehungsverhältnissen bewirkt werden, so müssen die beiden Scheibenkörper F k, Φκ, derartig stufenförmig abgedreht sein, daß der Treibriemen ohne Aenderung seiner Länge paßt, wenn derselbe auf je zwei entsprechende Ränder gelegt wird. In der Figur enthalten die beiden Scheibenkörper z.B. je sieben Stufen bezw. je sieben Scheiben. Die Radien r₁ ρ₁, r₂ ρ₂, r₃ ρ₃, ... je zwei entsprechender Scheiben müssen in dem umgekehrten Verhältnis der Umdrehungszahlen stehen und eine Größe besitzen, daß der Treibriemen für jedes Paar der entsprechenden Scheiben paßt. Zwei so hergestellte Scheibenkörper heißen Stufenscheiben.

Ist der Achsenabstand Φ F, der Radius ρ₁ der größten Scheibe der treibenden Stufenscheibe Φκ und deren Umdrehungszahl ω_t für eine angenommene Zeiteinheit gegeben; sind ferner die verschiedenen Umdrehungszahlen ω₁ ω₂ ω₃ ... der getriebenen Stufenscheibe F k gegeben, so ist zunächst durch das Verhältnis r₁/ρ₁ = ω_t/ω₁ der Radius r₁ der kleinsten Scheibe der Stufenscheibe F k und durch die Größen ρ₁, r₁, Φ F die Riemenlänge bestimmt Die übrigen entsprechenden Scheibenradien ρ₂, ρ₃ ... r₂ r₃ ... können dann vermitteln einer Hilfskurve ζ, die in großer Annäherung durch einen Kreisbogen ersetzt ist und Scheibendiagramm heißt, konstruiert werden. Zu diesem Zwecke wird eine Gerade M X unter Neigung von 45° gegen die Achse F' gezogen, die Länge M X = Φ F gemacht, dann die Senkrechte X B = ¹/₂ Φ F errichtet und mit dem Radius M B um M der Kreisbogen ζ beschrieben. Auf einer zur Achse F' senkrechten Geraden, die M X im Punkte m trifft, wird die Strecke m a = r₁ und a α = ρ₁ aufgetragen. Hierauf werden zu M X die Parallelen a R₁, α Z₁, von denen α Z₁ den Kreisbogen ζ in Z₁ trifft, gezogen; ferner wird durch Z₁ senkrecht zur Achse F' die Gerade Z₁ R₁ durch R₁ die Gerade R₁ A senkrecht a α bis an M X gezogen; und diese Gerade R₁ A wird mit dem Scheibendiagramm ζ so gelegt, daß sie sich in der verlängerten Achse F' befindet. Die Gerade A R₁ bis (+ r) verlängert wird als die Abszissenachse des Scheibendiagramms ζ genommen. Auf dieser Abszissenachse wird in einem beliebigen Punkte G eine Senkrechte G Q errichtet, die M A im Punkte Q schneidet. Auf dieser Senkrechten werden die Punkte Q₂, Q₃ ... so bestimmt, daß

GQ/GQ₂ = ωt/ω₂, GQ/GQ₃ = ω_t/ω₃ ...

ist. Dann werden von den Punkten Q₂, Q₃, Q₇ Gerade nach A gezogen, welche auf dem Kreisbogen ζ bezw. die Schnittpunkte Z₂, Z₃ ... bestimmen und[393] von diesen auf die Abszissenachse A (+ r) die senkrechten Ordinaten Z₂ R₂, Z₃ R₃ ... gezogen, welche die Gerade M A bezw. in den Punkten S₂, S₃ ... treffen. Hiernach sind, wenn man die ersten Werte r₁ ρ₁ mit aufschreibt, die Radien der Stufenscheiben r₁ = R₁ S₁, r₂ = R₂ S₂, r₃ = R₃ S₃, ... ρ₁ = R₁ Z₁, ρ₂ = R₂ Z₂, ρ₃ = R₃ Z₃ ..., und die durch S₁ S₂, S₃ ... zur Achse F' parallel gezogenen Geraden ergeben sich direkt für die Stufenscheibe F k die Scheibenradien r₁, r₂, r₃. Die Begründung dieser Konstruktion, bei welcher das Scheibendiagramm ζ mit großer Genauigkeit durch jenen sehr leicht zu bestimmenden Kreisbogen ζ, ersetzt werden kann, ist in [1] angegeben.

Literatur: [1] Burmester, L., Lehrb. d. Kinematik, Leipzig 1888, Bd. 1, S. 395.

Burmester.