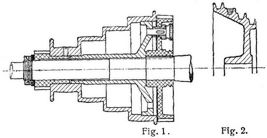
Stufenscheiben

Stufenscheiben enthalten nebeneinander die Bahnen von Schnur- oder Riemscheiben mit verschiedenem Durchmesser und ermöglichen durch Umlegen der Schnur oder des Riemens die stufenweise Aenderung der übertragenen Geschwindigkeit.

Sie finden nach Fig. 1, auch Riemenkonus genannt, vorzugsweise Anwendung bei Bohr- und Fräsmaschinen (Bd. 4, S. 176) und Drehbänken (Bd. 3, S. 8t); sie sitzen hier meist lose auf der Spindel zwischen den Lagern (Bd. 6, S. 52). Als Schnurscheiben kommen sie an kleinen Drehbänken (s. Bd. 3, S. 68) und Drehstühlen vor. Zum Umlegen der Schnur muß man die Scheiben etwas nähern, ebenso beim Keilriemen (Fig. 2), nicht aber beim Umlegen eines Riemens (s. Bd. 7, S. 429). – Ueber Stufenzahnräder s. [3].

Während für schmale Scheiben eine einfache Nabe nach Fig. 2 genügt, erhalten breitere eine am offenen Ende an- oder eingesetzte Stirnscheibe, deren Nabe in Fig. 1 [2] bis zum andern Ende durchgeht, ohne in ganzer Länge an der Welle aufzuliegen, weil sonst infolge der Verbiegung der Spindel Klemmungen entstehen können. – In der Regel läuft der Riemen auf zwei gleichen Kegeln, deren Bahnen mit gleichen Stufenhöhen abgesetzt werden; dabei wechselt die Uebersetzung angenähert in konstantem Verhältnis, und zwar beträgt dieses, wenn die kleinste Stufe halb soviel Durchmesser wie die größte erhält, für dreistufige Scheiben 0,5, bei vierstufigen 0,625 und in der Mitte 0,64, bei fünfstufigen 0,70 und inmitten 0,715. Der größte Durchmesser findet sich zu (6 ~ 8) √h für Drehbänke von h cm Spitzenhöhe, der kleinste zu (3 ~ 4) √h, die Breite der Bahn zu 1,5 √h, der Riemen um 1 cm schmäler.

Die Rücksicht auf gleiche Riemenlänge, nämlich auf gleiche Anspannung des Riemens in allen Lagen, bedingt eine Berichtigung der berechneten Durchmesser, so daß die Summe zweier zusammen arbeitender Stufendurchmesser D + d gegenüber der Summe 2 D₀ zweier gleichgroßen Scheibendurchmesser um so kleiner werde, je stärker das Uebersetzungsverhältnis D : d oder d : D und je geringer die Entfernung e der beiden Wellen ist, während für Kreuzriementrieb die Summen konstant bleiben. Die Riemenlänge beträgt für gleiche Scheiben 2 e + π D₀. Für ungleiche Scheiben mit offenen, schrägliegenden Riementrumen ergibt die geometrische Berechnung auf gleiche Länge die Beziehung 2D₀/D + d = 1 + D + d/2πe(D : d – 1/D : d + 1)². Hiernach ist die Summe D + d gegen 2 D₀ um so viel Prozent, wie die Tabelle angibt, zu verkleinern.

Zum Beispiel für D : d oder d : D = 1

Zum Beispiel für ein Paar Stufenscheiben von 200–400 mm Durchmesser bei 2 m Wellenabstand ist D₀ = 300 mit e : D = 7 und für die äußeren Stufen D : d oder d : D = 2; nach der Tabelle hat man die Stufen um 0,5% zu berichtigen, so daß sie auf 199–300–398 mm oder auf 200–301,5–400 mm kommen.

Literatur: [1] Lehrbücher über Werkzeugmaschinen. – [2] Perrigo, Modern American Lathe Practice, New York 1907 (S. 301), und Merlot, Machines-outiles, Paris et Liege 1907 (S. 159). – [3] Zeitschr. d. Ver. deutsch. Ing. 1907, S. 1491–1627.

Lindner.

Fig. 1., Fig. 2.