Verwandlung von Flächen

Verwandlung von Flächen. Um den Flächeninhalt geschlossener ebener Figuren zu messen, verwandelt man diese zuweilen auf zeichnerischem Wege in gleich große einfachere Figuren, in der Regel in Dreiecke oder Vierecke.

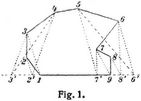
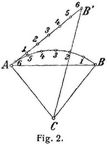
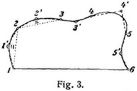
Um beispielsweise das Neuneck 1 2 3 ... (Fig. 1) in ein Viereck gleicher Größe zu verwandeln, zieht man parallel zu 1 3 die Linie 2 2', parallel zu 2' 4 die Linie 3 3'; ebenso auf der rechten Seite 8 8' || 7 9, 7 7' || 6 8' und 66' || 57'; dann ist 3' 4 5 6' das gesuchte Viereck. Das Verfahren stützt sich auf den bekannten Satz, daß der Flächeninhalt eines Dreiecks unverändert bleibt, wenn man die Spitze parallel zur Grundlinie verschiebt. – Um den Kreisausschnitt ABC (Fig. 2) zu messen, streckt man den Bogen A B auf die Tangente A B', indem man mit einer nicht zu großen Zirkelöffnung von B gegen A und hierauf um ebenso viele[790] Schritte von A gegen B' wandert. Dann ist der Kreisausschnitt gleichgroß wie das Dreieck AB' C. Ferner ist der Flächeninhalt des Kreisabschnittes A B gleich dem des überschlagenen Viereckes A B' C B. – Den Flächeninhalt einer krummlinig begrenzten, unregelmäßigen Figur (Fig. 3) bestimmt man, indem man die krumme Linie in Stücke 1 2, 2 3, 3 4 u.s.w. zerlegt, die man genau genug als Parabeln ansehen kann. Dann verwandelt man die Abschnitte 1 2, 2 3 u.s.w. in Dreiecke, indem man je ein Drittel der Abschnitthöhe nach außen anfügt. So ist das Dreieck 1 1' 2 gleich dem Abschnitte 1 2. Es entsteht hierbei ein Elfeck 1 1' 2 2' 3 ..., das man schließlich wie oben auf ein Viereck überführen kann. Den Inhalt eines Vierecks findet man als Summe zweier Dreiecke, die eine Diagonale des Vierecks als gemeinsame Grundlinie haben.

Literatur: Culmann, Graphische Statik, Zürich 1875; Ott, v., Grundzüge des graphischen Rechnens, Prag 1884; Keck, Vorträge über graphische Statik, Hannover 1894; Lauenstein, Graphische Statik, Stuttgart 1898.

Mörsch.

Fig. 1.

Fig. 2.

Fig. 3.