Zahnexzentrik

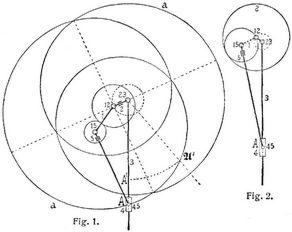
Zahnexzentrik ist ein in Fig. 1 schematisch dargestellter Mechanismus, der zwei in einem Gliede 1 gelagerte und im Eingriff befindliche Zahnräder 2, 5 enthält, von denen das Zahnrad 2 durch eine Achse 23 mit dem stangenförmigen Gliede 3 drehbar verbunden und das Zahnrad 5 durch die Achse 45 an eine auf 3 gleitende Hülse 4 drehbar angeschlossen ist [1]. Wird das stangenförmige Glied 3 als fest betrachtet, dann heißt dieser Mechanismus ein Zahnexzentrikgetriebe.

Das Zahnrad 2 dreht sich bei diesem Getriebe in dem seiten Gliede 3 um die feste, exzentrische Achse 23; dadurch wird das Glied 1, in welchem sich die Räderachsen 12, 15 befinden, und das Zahnrad 5 nebst der mit demselben einstückig verbundenen Stange 15-A in Bewegung versetzt, durch welche eine schwingende Bewegung der auf 3 gleitenden Hülse 4 bewirkt wird. Bei der in Fig. 2 dargestellten Anordnung ist das um die feste, exzentrische Achse 23 rotierende Zahnrad 2 ein Hohlrad, in welchem das Zahnrad 5 läuft.

Um in Fig. 1 die komplizierte schwingende Bewegung des Gliedes 4 auf der Stange 3 zu veranschaulichen, betrachten wir einstweilen das Zahnrad 2 als seit und denken uns das Glied 1 um die jetzt feste Achse 12 gedreht; dann beschreibt der mit dem umlaufenden Rade 5 verbundene Punkt A, der mit dem Achsenpunkt 45 identisch ist, eine zyklische Kurve (s. Bd. 6, S. 17), die im betrachteten Falle eine verschlungene Epizykloide a ist und von zwei rechtwinkligen Geraden symmetrisch geteilt wird. Die Stange 3 rotiert hierbei um die feste Achse 23. Stellen wir jetzt wieder das Glied 3 seit und denken wir uns die Epizykloide a mit dem um die feste, exzentrische Achse 23 rotierenden Zahnrade 2 verbunden, dann bewegt sich der Schnittpunkt A, welchen die[959] bewegte Epizykloide a mit der festen Geraden 3 bildet, ebenso wie die Hülse 4 auf der Stange 3. Dreht sich z.B. das Zahnrad 2 mit der Epizykloide a in dem Sinne A¹ A¹ um den Winkel A¹-23-A¹, so wird, wenn 23-A¹ = 23-A¹ gemacht ist, der Punkt A während dieser Drehung nach A¹ bewegt. So vielmal wie der mit dem Radius 23-A¹ um 23 beschriebene Kreis die Epizykloide a schneidet, so oft wird der Punkt A während einer Umdrehung des Rades 2 an die Stelle A¹ gelangen [2]. In Fig. 1 ist beispielsweise für das Verhältnis der Rollkreisradien der Zahnräder 5, 2 das einfache Verhältnis 1 : 2 gewählt. Wenn dieses Verhältnis weniger einfach ist, dann wird der Schwingungsvorgang der Hülse 4 noch viel komplizierter. In Fig. 2 ist ebenfalls das Verhältnis der Rollkreisradien des Vollrades 5 und des Hohlrades 2 gleich 1 : 2 angenommen. Denken wir uns auch in diesem Falle einstweilen das Zahnrad 2 festgestellt, dann würde der mit dem Rade 5 verbundene Punkt A eine Hypozykloide beschreiben, die bei diesem Verhältnis eine Ellipse mit dem Mittelpunkt 12 ist (vgl. Cardanische Kreise). Wenn wir dann wieder das Glied 3 als seit betrachten und uns diese Ellipse mit dem rotierenden Rade 2 verbunden denken, dann wird durch dieselbe in gleicher Weise wie durch jene Epizykloide a in Fig. 1 der Schwingungsvorgang der Hülse 4 veranschaulicht [3].

Literatur: [1] Reuleaux, Zahnexzentrik, Zivilingenieur, Bd. 4, S. 4, 1858. – [2] Burmester, Lehrbuch der Kinematik, Bd. 1, S. 524, Leipzig 1888. – [3] Rittershaus, Untersuchung dieses in andrer Gestaltung bei der Wanzerschen Nähmaschine angewandten Mechanismus, Zivilingenieur, Bd. 26, S. 27, 1880.

Burmester.

Fig. 1., Fig. 2.