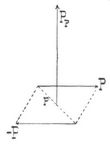
Achsenmoment eines Paares

Achsenmoment eines Paares. Ein Streckenpaar, z.B. ein Kräftepaar oder ein Rotationspaar von Winkelgeschwindigkeiten (P, –P), hat ein Moment gleich der Fläche Pp des Parallelogramms, das von den Strecken des Paares gebildet wird. Da das Paar stets einen bestimmten Sinn (Uhrzeigersinn oder diesem entgegengesetzten) hat, so tritt das Moment mit einem bestimmten positiven oder negativen Zeichen in die Rechnung ein. Man stellt daher den Zahlenwert des Momentes durch eine Länge dar, die man auf dem irgendwo auf der Ebene des Paares errichteten Perpendikel aufträgt, mit einer Pfeilspitze versehen, die nach derjenigen Seite der Paaresebene in den Raum hineinzeigt, von wo aus ein Auge den Sinn des Paares mit der Uhrzeigerbewegung harmonierend erkennt (s. die Figur). Diese gerichtete Strecke (Vektor) heißt das Achsenmoment des Paares, und sie enthält alle für die Wirkung des Paares wesentlichen Bestimmungsstücke. Würde man die Fläche des Parallelogramms in ein Parallelogramm verwandeln, dessen Höhe gleich der Längeneinheit ist, so stellt die Grundlinie des letzteren die Länge des Achsenmomentes dar.

Das Achsenmoment ist deswegen von Wichtigkeit, weil es die Zusammensetzung der Paare erleichtert. Die Resultante eines Systems von Achsenmomenten (Schlußlinie des Polygons der Achsenmomente) ist das Achsenmoment des den Paaren äquivalenten Paares und liefert daher unmittelbar das resultierende Paar selbst. Poinsot hat zuerst die Paare als besonderes Element in die Mechanik eingeführt [1] und durch deren Achsenmomente die Analogie nachgewiesen, die zwischen der Reduktion der Einzelstreckensysteme und der Reduktion von Paaren besteht.

Literatur: [1] Poinsot, L, Elements de statique, Paris 1848. – [2] Schell, W., Theorie der Bewegung und der Kräfte, 2. Aufl., Leipzig 1879/80.

(Schell.) Finsterwalder.