- Cardanische Kreise
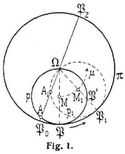
Cardanische Kreise. In Fig. 1 rollt ein Kreis p innerhalb an einem doppelt so großen festen Kreise π. Gelangt der rollende Kreis p aus seiner Lage, in der er den Kreis π im Punkt P berührt, nach p1 und der Berührungspunkt nach P1 so ist, wenn man im Kreise π den Radius ΩP1 zieht, der den Kreis p in Punkt P trifft, der Bogen PP' auf dem gleich langen Bogen PP1 entlang gerollt. Zieht man ferner im Kreise π einen Durchmesser P0P2, der die Kreise p, p1 in den Punkten A, A1 schneidet, dann ist der Bogen AP gleich dem Bogen A1P1. Hieraus folgt, daß der Punkt A des rollenden Kreises p sich auf dem Durchmesser P0P2 nach A1 bewegt hat und daß jeder Punkt des rollenden Kreises p sich auf einem entsprechenden Durchmesser des festen Kreises π bewegt. Befindet sich der Berührungspunkt des rollenden Kreises p in P0, dann koinzidiert der Punkt A mit P0. Während der Kreis p von P0 bis P2 und ferner von P2 bis P0 rollt, durchläuft demnach der Punkt A des rollenden Kreises p den Durchmesser P0P2 hin und her gehend. Dasselbe gilt von allen Punkten des rollenden Kreises. Diesem von Cardano [1] mitgeteilten Bewegungsvorgang entsprechend, hat man diese beiden Kreise Cardanische Kreise [2] genannt.
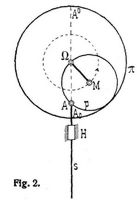
[424] Von De la Hire [3] wurde nachgewiesen, daß jeder mit dem rollenden Kreise verbundene Punkt, der nicht auf der Peripherie dieses Kreises liegt, eine Ellipse beschreibt, deren Mittelpunkt Ω ist [4] (s. Bewegung). Für den Mittelpunkt M des rollenden Kreises p geht die Ellipse in den um Ω beschriebenen Kreis p über. Betrachten wir in Fig. 2 den Kreis π als Teilkreis eines innen verzahnten, festen Radkranzes, ferner den rollenden Kreis p als Teilkreis eines Zahnrades p, das in den festen Radkranz eingreift; ist ΩM ein um die feste Achse Ω rotierender Arm, in dem die Achse M des Zahnrades p gelagert ist, dann wird bei Umdrehung des Armes der Punkt A des Zahnrades p auf dem Durchmesser A0A° des Kreises π hin und her gehen. Eine Stange s, die auf einem in A an dem Zahnrade p befestigten Zapfen drehbar gehängt ist und in einer festen Hülfe H gleitet, wird während der Umdrehung des Armes ΩM hin und her bewegt. Diese geradlinige Bewegung, die bei der König & Bauerschen Buchdruckschnellpresse [5] angewendet ist, wird hypocykloidische Geradführung genannt.
Literatur: [1] Cardanus, Opus novum de proportionibus numerorum, motuum etc., Basil. 1570, prop. 173, p. 186. – [2] Reuleaux, Kinematik, Braunschweig 1875, S. 124. – [3] Memoires de l'Académie, Paris 1706, p. 351. – [4] Burmester, Lehrbuch der Kinematik, Leipzig 1888, Bd. 1, S. 37. – [5] Hülße, Allgem. Maschinenencyklopädie, Leipzig 1844, Bd. 2, S. 772.
Burmester.
http://www.zeno.org/Lueger-1904.