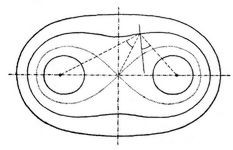
- Cassinische Kurven
Cassinische Kurven (Cassinische Ovale). Eine solche ist der Ort eines Punktes, dessen Entfernungen von zwei gegebenen festen Punkten, den sogenannten Brennpunkten der Kurve, ein konstantes Produkt liefern.
Nimmt man die Mitte zwischen den Brennpunkten, deren Entfernung 2 a sein möge, zum Ursprung, ihre Verbindungslinie zur x-Achse eines rechtwinkligen Koordinatensystems und bezeichnet man mit c2 jenes konstante Produkt, so wird die Gleichung der Kurve
(x2 + y2)2 – 2 a2 (x2 – y2) + a4 – c4 = 0.
oder in Polarkoordinaten r, φ
r4 – 2a2r2 cos 2φ + a4 – c4 = 0.
Die Kurve ist zu beiden Achsen symmetrisch (hat also einen Mittelpunkt im Ursprung) und besteht entweder aus zwei getrennten Ovalen oder einem einzigen geschlossenen Zuge, je nachdem c < a oder c > a ist. In dem Uebergangsfall (in der Figur punktiert) c = a heißt sie Lemniskate. Die Normale der Kurve in irgend einem Punkt bildet mit einem der beiden Brennstrahlen denselben Winkel, wie der andre Brennstrahl mit der Linie von jenem Punkt nach dem Mittelpunkt der Kurve. – Weitere Eigenschaften und Literatur in: G. Loria, Spezielle algebraische und transzendente ebene Kurven, deutsche Ausgabe von Fr, Schütte, Leipzig 1902, S. 193.
Mehmke.
http://www.zeno.org/Lueger-1904.