Doppelschwinggetriebe

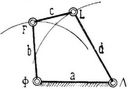
Doppelschwinggetriebe. Zwei Glieder Φ F, Δ L (s. die Figur), die in dem festen Gestell Φ Δ resp. um die parallelen Achsen Φ, Δ schwingen und durch eine Koppel F L vermittelst der ebenfalls parallelen Achsen F, L gelenkig verbunden sind, bilden, wenn die beiden Glieder Φ F, Δ L infolge dieser Verbindung nur schwingen können, mit dem Gestell und der Koppel ein Doppelschwinggetriebe, das auch kurz Doppelschwinge genannt wird [1].

Schwingungen, d.h. nicht vollständige Umdrehungen, dieser beiden Glieder treten nur dann auf, wenn die Summe der kleinsten und der größten Gliedlänge nicht größer als die Summe der beiden andern Gliedlängen ist und das Glied, das dem kleinsten Glied gegenüber liegt, das feste Gestell vertritt. In vorstehender Figur ist z.B. c das kleinste, d das größte Glied und c + d < a + b.

Literatur: [1] Burmester, Lehrbuch der Kinematik, Leipzig 1888, Bd. 1, S. 291. – [2] Grashof, Theoretische Maschinenlehre, Leipzig 1883, Bd. 2, S. 114.

Burmester.