- Evolvente
Evolvente einer Kurve (Grundkurve) wird beschrieben von einem Punkte einer Tangente der Grundkurve, wenn erstere auf letztere ohne zu gleiten rollt. Die unendlich vielen Evolventen einer Kurve sind gegenseitige Parallelkurven.
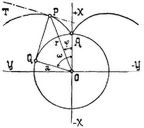
Die Differentialgleichung der Evolventen der Kurve y = f(x) in ξ, η ergibt sich durch Elimination von x aus: η – f(x) = f'(x) (ξ – x); f'(x) dη/dξ + 1 = 0. Ist x sinφ – y cosφ = p(φ) die Hessesche Normalform der Tangente einer Kurve, so ergibt die Elimination von y aus dieser Gleichung und der durch Integration erhaltenen: – x cos φ – y sin φ = ∫ p(φ)dφ die Evolvente. Die Grundkurve kann als Evolute der Evolvente angesehen werden; daher liegen die Krümmungsmittelpunkte der Evolvente auf der Grundkurve. Die Evolvente hat Rückkehrpunkte in den Wendepunkten der Grundkurve. – Die Evolvente des Kreises, Kreisevolvente genannt (s. die Figur), hat die Gleichung:
oder in Parameterdarstellung
wobei a der Radius des gegebenen Kreises ist. Es ist PQ = Bogen AQ. Die Tangente PT ist parallel zum Radius OQ. Die Fußpunktkurve der Kreisevolvente mit dem Kreismittelpunkt als Pol ist eine archimedische Spirale. Die Sektorfläche POA ist 1/6a2ω3 der Bogen PA ist r2 – a2/2a.
Wölffing.
http://www.zeno.org/Lueger-1904.