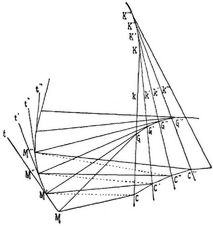
Fadenkonstruktion von Huyghens-Monge

Fadenkonstruktion von Huyghens-Monge. Man kann durch eine geometrische Konstruktion einen Punkt nötigen, jede beliebig gegebene Kurve zu beschreiben. Für ebene Kurven hat Huyghens diese Konstruktion gefunden, für doppelt gekrümmte Kurven hat Monge dieselbe angegeben.

Wir wollen zunächst die Mongesche Konstruktion als die allgemeinere entwickeln und hierauf die Huyghenssche als einen speziellen Fall dieser behandeln. Es seien (s. die Figur) M, M', M'', M''' ... eine Folge unendlich naher Punkte einer Kurve, t, t', t'', t''' ... die Tangenten in ihnen, welche die Richtungen der Bogenelemente MM', M'M'', M''M''' ... find; v, v', v'', v''' ... die zu den Tangenten senkrechten Normalebenen und σ, σ', σ'', σ''' ... die Schmiegungsebenen MM'M'', M'M''M''' ..., welche drei aufeinander folgende Punkte oder, was dasselbe ist, zwei aufeinander folgende Tangenten enthalten. Die Schmiegungsebenen enthalten die Krümmungskreise in M, M', M'' ..., und die Normalebenen schneiden sich der Reihe nach in Geraden k, k', k'' ..., die in den Mittelpunkten C, C', C'', C''' ... der Krümmungskreise auf den Schmiegungsebenen senkrecht stehen und die Krümmungsachsen in M, M', M'', M''' ... heißen. Da die Krümmungsachsen[562] aufeinander folgend in den Normalebenen liegen, so schneiden sie sich in Punkten K, K', K'', K''' ..., die eine Kurve bilden, deren Tangenten sie sind. Sie erzeugen eine abwickelbare Fläche, und die Normalebenen, deren jede durch drei aufeinander folgende Punkte dieser Kurve gehen, sind die Tangentenebenen dieser Fläche und die Schmiegungsebenen dieser Kurve, die auf der Fläche eine scharfe Kante bildet (Rückkehrkante, Gratlinie, Arete de rebroussement). Jede Normalebene v enthält ein Strahlenbüschel von Normalen der Kurve M mit M als Scheitel. Die Normale n, die in die Schmiegungsebene σ des Punkts M fällt, heißt die Hauptnormale im Punkte M; sie geht durch den Krümmungsmittelpunkt C hindurch. Die Hauptnormale n, n', n'' ... bilden eine windschiefe Fläche; denn die Hauptnormalen schneiden sich nicht, da sie in den aufeinander folgenden Schmiegungsebenen liegen, die sich aufeinander folgend in den Tangenten t der Kurve M M' M'' ... schneiden. Die Fläche der Hauptnormalen enthält die Kurve M M' M'' ... und die Kurve C C' C'' ... der Krümmungsmittelpunkte; die Fläche der Krümmungsachsen enthält die Kurve C C C' » ... der Krümmungsmittelpunkte und die Gratlinie K K K'« ...; die Erzeugungslinien beider Flächen, nämlich die Hauptnormalen und die Krümmungsachsen, schneiden sich in den Krümmungsmittelpunkten rechtwinklig.

Da die Krümmungsachse k im Krümmungsmittelpunkte C auf der Schmiegungsebene, der Ebene des Krümmungskreises, senkrecht steht, so ist jeder ihrer Punkte G Mittelpunkt eines Rotationskegels, der durch den Krümmungskreis geht, und hat von drei Punkten M, M', M'' der Kurve gleichen Abstand GM = GM' = GM''. Von ihm aus können daher die beiden Bogenelemente M M' und M' M'' der Kurve beschrieben werden, die der Krümmungskreis mit dieser gemein hat. Ziehen wir jetzt von M nach irgend einem Punkt G der Krümmungsachse k die Normale MG, sodann von M' durch G die Normale M'G', welche die folgende Krümmungsachse k' in G' trifft; ebenso von M'' durch G' die Normale M'' G'', welche k'' in G'' begegnet u.s.w., so erhalten wir auf der Fläche der Krümmungsachsen eine Kurve G G' G'' ..., deren Tangenten die Normalen in M sind und deren Schmiegungsebenen durch die Tangenten t gehen und also auf den Normalebenen, d.h. den Tangentenebenen der Fläche der Krümmungsachsen, senkrecht stehen. Spannt man daher einen vollkommen biegsamen Faden von M nach G, biegt ihn über die Kurve G G' G'' ... hin und hebt sodann denselben von dieser Kurve allmählich ab, so daß er tangential an sie bleibt, so beschreibt der Punkt M die Kurve M M' M'' ... Da der Punkt G auf der Krümmungsachse k beliebig gewählt werden kann, so kann die Kurve M M' M'' ... auf unzählige Arten durch diese Fadenkonstruktion beschrieben werden. Die Kurven G G' G'' ... heißen die Evoluten der Kurve M M' M'' ...; jede Kurve hat daher unendlich viele Evoluten, die sämtlich auf der Fläche der Krümmungsachsen liegen. Diese Fläche heißt die Evolutenfläche der Kurve M M' M'' ... Um alle Unsicherheit in der Bewegung des Fadens beim Abheben von der Evolute zu vermeiden, spannt Monge, dem man diese Konstruktion verdankt, zwei Fäden, je einen über eine Evolute und verknüpft sie in dem Punkt M, der die Kurve beschreibt. Der Evolute gegenüber heißt die Kurve M M' M'' ... Evolvente. Es beschreibt aber jeder Punkt M des gespannten Fadens eine Evolvente. Alle diese Evolventen haben gemeinschaftliche Fläche der Evoluten.

Ist die Kurve eben, so fallen alle Schmiegungsebenen in der Ebene der Kurve zusammen, die Krümmungsachsen werden alle parallel und die Fläche der Evoluten wird eine Zylinderfläche. Die Kurve der Krümmungsmittelpunkte, die im allgemeinen Falle keine Evolute ist, weil ihre Tangenten nicht durch die Punkte der Kurve M M' M'' ... hindurchgehen, wird in diesem Falle eine Evolute, nämlich diejenige, die gewöhnlich als Evolute der ebenen Kurve bezeichnet wird. Sie ist die einzige ebene Evolute, während alle andern Evoluten Schraubenlinien auf dem Evolutenzylinder sind. Die Theorie der ebenen Evoluten ist von Huyghens begründet worden bei Gelegenheit seiner Untersuchungen über das Cykloidenpendel.

Ist die Kurve sphärisch, so gehen alle Normalebenen durch den Mittelpunkt der Kegelfläche, der die Kurve angehört, und diese Normalebenen schneiden sich in den Krümmungsachsen, die eine Kegelfläche erfüllen. Die Gratlinie K K' K'' ... reduziert sich auf den Mittelpunkt der Kegelfläche. Ist die Kurve weder eben noch sphärisch, so ist die Evolutenfläche eine allgemeine abwickelbare Fläche, und die Evoluten bilden auf ihr, wie leicht erwiesen werden kann, das System der kürzesten Linien.

Literatur: Monge, Application de l'analyse a la geometrie, 5. edit. par Liouville, Paris 1850, S. 392–406; Hugenii opera varia, Vol. I, Lugduni Batav. 1724 (Horologium oscillatorium, sive de motu pendulorum ad horologia aptato demonstrationes geometricae, Pars III, De linearum curvarum evolutione et dimensione, S. 90). – Schell, Allgemeine Theorie der Kurven doppelter Krümmung, 2. Aufl., Leipzig 1898, S. 48–59.

(Schell) Finsterwalder.