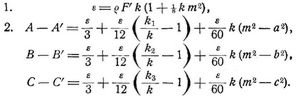- Geodätische Dreiecke
Geodätische Dreiecke nennt man Dreiecke auf der mathematischen Erdoberfläche (allgemein auf jeder beliebigen krummen Fläche), deren Seiten die kürzenden Linien (geodätische Linien) zwischen den Eckpunkten sind und deren Winkel von den in den Eckpunkten an die geodätischen Linien gelegten Tangenten gebildet werden.
Die wichtigsten Sätze über die geodätischen Dreiecke werden durch die folgenden Formeln zum Ausdruck gebracht, die das geodätische Dreieck zu einem ebenen Hilfsdreieck von gleicher Seitenlänge in Beziehung setzen:
Darin bedeuten ε den Exzeß, a, b, c die Dreieckseiten des geodätischen und ebenen Hilfsdreiecks, A, B, C die Winkel des ersteren, A', B', C' die Winkel des letzteren, F' den Flächeninhalt des letzteren, m2 = a2 + b2 + c2/3 das arithmetische Mittel der Quadrate der Dreieckseiten, k1, k2, k3 das Krümmungsmaß für die drei Eckpunkte des Dreiecks, k = (k1 + k2 + k3)/3 das arithmetische Mittel derselben gültig für die gesamte Fläche des betreffenden Dreiecks. Die allgemeine Gleichung für das Krümmungsmaß ist:
worin r der mittlere Krümmungsradius, RI und RII die Hauptkrümmungsradien und φ die Polhöhe für die betreffenden Ellipsoidpunkte und e die Exzentrizität, a0 die große Halbachse des Ellipsoides bedeuten. In den Gleichungen 2. drückt das zweite Glied auf den rechten Seiten den Einfluß der Abplattung des Ellipsoides auf die Krümmung in den Eckpunkten aus (fällt also für sphärische Dreiecke weg), das dritte Glied den Einfluß des Unterschiedes der Seitenlängen. Die numerische Auswertung der Gleichungen zeigt, daß für alle direkt meßbaren geodätischen Dreiecke der Einfluß des zweiten und dritten Gliedes weit innerhalb der Grenzen der Beobachtungsfehler bleibt und bei den Rechnungen für eine Landesvermessung die sphärischen Formeln im allgemeinen hinreichend sind (vgl. Triangulierung). Für spezielle Aufgaben der Erdmessung, z.B. für große Dreiecke, deren Seiten aus Dreiecksketten abgeleitet werden, finden die Gleichungen praktische Anwendung. Die Theorie der geodätischen Dreiecke ist begründet von Gauß [1].
Literatur: [1] Gauß, Disquisitiones generales circa superficies curvas, Göttingen 1828. – Weiteres s. [2] Helmert, Die mathematischen und physikalischen Theorien der höheren Geodäsie, Leipzig 1880, Bd. 1, S. 346, sowie [3] Jordan, Handb. d. Vermessungskunde, Stuttgart 1906, Bd. 3, § 90–96. – In [2] und [3] ist die weiter in Frage kommende Literatur angegeben.
Reinhertz.
http://www.zeno.org/Lueger-1904.