Höhenwinkel

Höhenwinkel, in der Geodäsie und sphärischen Astronomie der Winkel zwischen einer Zielrichtung und ihrer vertikalen Projektion auf den Horizont. In der Praxis der Messung von Höhenwinkeln tritt sehr häufig an seine Stelle die Zenitdistanz, welche den Höhenwinkel zu 90° ergänzt (h = 90° – z).

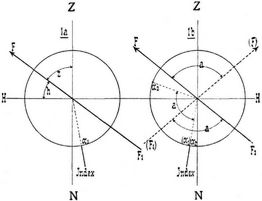
Je nach dem Zweck der Höhenwinkelmessung und der dadurch bedingten Genauigkeit richtet sich die Anwendung sehr verschiedener Instrumente. Für einfache geodätische Aufnahmen gebraucht man Gradbögen, an denen die Richtung der Visierlinie gegen den Horizont mit Hilfe von Pendeleinrichtungen oder mittels Libellen abgelesen werden kann (z.B. die Neigung von gemessenen Linien gegen den Horizont, um deren Längen auf den Horizont reduzieren zu können oder um genäherte Höhenbestimmungen von terrestrischen Objekten zu erhalten, deren Entfernung man kennt). Weiterhin werden Schrauben zu solchem Zwecke verwendet, für die der Winkelwert einer Umdrehung bekannt ist (beim Nivellierinstrument [Stampfer] oder auch in der Tachymetrie [s.d.]). – Für genauere derartige Messungen, und wenn solche auch für größere Höhen bestimmt sein sollen, verwendet man dann die Höhenkreise an den Kippregeln oder den Theodoliten (s.d.), und für die genauesten derartigen Messungen, wie sie für die Zwecke[99] der höheren Geodäsie und der Astronomie nötig werden, kommen die großen Universalinstrumente, Höhenkreise, Meridiankreise u.s.w. in Verwendung. Die Methoden zur Messung von Höhenwinkeln sind vor allem bedingt durch die Art des anvisierten Objektes, d.h. ob dasselbe ein feststehendes (irdisches) oder ein mit der Zeit seinen Ort änderndes (meist cölestisches – Gestirn – oder etwa ein Luftballon oder dergl.) ist. Davon wird es abhängen, ob man an dem benutzten Instrument direkt die der genauen Horizontal- oder Vertikalrichtung entsprechende Ablesung kennen muß oder ob sie, wie im ersteren Falle, durch die Art der Messung nicht nur eliminiert, sondern ihre Kenntnis sogar überflüssig wird, was allerdings nicht ausschließt, daß man den sogenannten Zenitpunkt oder Horizontpunkt des Kreises mit bestimmt, um eine Kontrolle für das Instrument zu erhalten. Des weiteren werden diesen beiden Arten der Höhenwinkelmessung verschiedene Korrektionen wegen Refraktion (s.d.) zuerteilt werden müssen. Die durch die Aufteilung und die Konstruktion der Instrumente bedingten Korrektionen (Instrumental- resp. Aufstellungsfehler) werden aber in beiden Fällen in gleicher Weise zur Wirkung kommen. – Um nun zu erläutern, wie man an einem Kreise, dessen Ebene vertikal steht, einen Höhenwinkel zu messen pflegt, denke man sich in der Figur die schematische Darstellung des Kreises mit seiner von 0 bis 360° durchgehenden Teilung; mit diesem Kreise fest verbunden mag das Fernrohr sein, dessen Zielrichtung die Linie F F₁ zur Anschauung bringt. Weiterhin sei an irgend einer Stelle des Instruments der zum Ablesen des Kreises dienende Index so angebracht, daß seine Lage gegenüber den übrigen Teilen des Instruments auch bei dessen Drehung um eine vertikale Achse konstant bleibt oder daß die Verbindungslinie des Index mit der Kippachse des Fernrohres resp. mit dem Zentrum des Kreises gegen den Horizont eine konstante Neigung hat. Ist außerdem H–H eine durch das Zentrum des Kreises gelegte Horizontale, so wird ZN die Vertikale im Beobachtungsort sein und somit der Winkel z = 90 – h die Zenitdistanz der Zielrichtung F F₁. Macht man nun in der in 1 a dargestellten Lage des Instruments eine Ablesung des Kreises am Index vom Betrage α₁, dreht darauf das Instrument um die Vertikalachse um 180°, so wird die Richtung der Visierlinie die in 1 b gestrichelt dargestellte sein, während sich in der Lage der Instrumententeile zueinander gar nichts geändert hat. Um nun das Fernrohr wieder in die Richtung nach dem zuerst anvisierten Objekte zu bringen, muß man dasselbe offenbar um den Winkel a im Sinne des Pfeiles drehen; um diesen Betrag a wird sich daher auch die Ablesung α₂ der Kreise am Index geändert haben müssen. Also hat man a = α₂ – α₁ und dieser Winkel entspricht, wie sofort einzusehen ist, bei der oben vorausgesetzten Annahme der doppelten Zenitdistanz des Objektes, also

a = α₂ – α₁ = 2z = 2 (90 – h) = 180° – 2h

oder

z = 90 – h = (α₂ – α₁)/2.

Außerdem folgt aus dieser einfachen Betrachtung, daß die Lage des Index an sich ganz gleichgültig ist und daß man diejenige Stelle am Kreis erhalten wird, welche der Richtung des Fernrohres nach dem Zenit entspricht, wenn man das Mittel aus α₂ und α₁ bildet (eventuell die eine Zahl vermehrt um 360° für den Fall, daß der Index bei der Drehung des Fernrohres über den Nullpunkt des Kreises hinweggegangen ist), d.h. es ist

Zenitpunkt = (α₁ + α₂)/2 oder = (α₁ + α₂)/2 + 180°.

Nach diesen für jede Höhenmessung prinzipiellen Erläuterungen werden sich im speziellen die Ausdrücke sofort angeben lassen für die Fälle andrer Bezifferung der Höhenkreise, z.B. für zweimal von 0–180° oder für viermal von 0–90° und auch dann, wenn die Richtung der Bezifferung variiert. – Im allgemeinen sind die Indices zur Kreisablesung in Form von Verniers (Nonien) oder Mikroskopen ausgeführt, und dieselben sind zur Bequemlichkeit der Messung auch so angebracht, daß an ihnen entweder genäherte Zenitdistanzen oder Höhen direkt abgelesen werden für den Fall, daß solche Messungen nur in einer Kreistage ausgeführt werden sollen. (Nur bei Messungen untergeordneter Art zulässig.) Um die Lage der Ablesevorrichtung jederzeit kontrollieren oder eine Abweichung derselben von der Sollstellung in Rechnung ziehen oder korrigieren zu können, ist mit derselben fast stets eine mehr oder weniger empfindliche Libelle verbunden. In manchen Fällen ist auch mit dem Fernrohr selbst eine Libelle derart verbunden, daß diese einspielt, wenn die Fernrohrabsehenslinie horizontal steht (Kippregel oder Tachymetertheodolite). Die Justierung dieser Lage hat nach den Regeln der Tachymetrie (s.d.) zu erfolgen. – Dann braucht man nur eine Ablesung des Kreises (oder nur der meist vorhandenen Sektoren) zu machen bei einspielender Libelle und bei der Richtung des Fernrohres nach dem Objekt. Die Differenz gibt unmittelbar den Höhenwinkel. Die Abweichung der Kreisablesung bei horizontaler resp. vertikaler Visierrichtung von Null nennt man den Indexfehler, wenn das Instrument so eingerichtet ist, daß direkt Höhen- oder Zenitdistanzen abgelesen werden sollen. Der Betrag dieses Fehlers ist dann an die direkte Kreisablesung anzubringen; er wird bestimmt, indem man das Fernrohr, wie eingangs beschrieben, in beiden Lagen des Kreises (Kreis »Rechts« und Kreis »Links«) auf ein festes, gut sichtbares irdisches Objekt richtet, die Ablesungen α₁ und α₂ macht; deren Mittel soll 0° oder 180° sein, die Abweichung davon ist dann der »Indexfehler«.

[100] Ist das Objekt der Messung ein bewegtes (cölestisches, ein Stern oder dergl.), so gilt die Regel z = (α₂ – α₁)/2 nicht mehr, denn der Höhenwinkel hat sich in der von der ersten bis zur zweiten Einstellung verstrichenen Zeit geändert. Man muß also dann stets den Zenit- resp. Horizontpunkt kennen, wenn man die einzelnen Zenitdistanzen ableiten will. Es sind dann, wenn nach obigem der Zenitpunkt α_z gefunden worden ist, die einzelnen Zenitdistanzen für die Ablesungen entweder

α_z – α oder α – α_z,

je nachdem in Kreistage »rechts« oder »links« (resp. umgekehrt) beobachtet worden ist. Sind die Beobachtungen symmetrisch auf beide Lagen verteilt, so wird aus dem Mittel aller Zenitdistanzmessungen ein Fehler in der Annahme des Zenitpunktes wieder herausfallen, und es ist deshalb gestattet, diese Annahme auf ganze Minuten behufs einfacher Rechnung abzurunden. – Die nach dem eben beschriebenen Verfahren gemessenen Zenitdistanzen oder Höhen sind aber noch mit Fehlern behaftet, die entweder von der unrichtigen Aufstellung des Instruments oder von den Einflüssen der Atmosphäre herrühren. Die ersteren lassen sich durch die Methode der Anordnung der Beobachtungen entweder bestimmen oder wegschaffen. Der Einfluß der Achsenfehler und der Aufstellungsfehler ist aber auch, sobald es sich nicht um kleine Zenitdistanzen (große Höhen) handelt, sehr gering, wie die Formel für eine solche Korrektion Δ z zeigt:

Δ z = (c² + i²)/2 ctg z + ci cosec z.

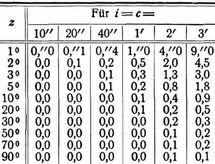
Die Auswertung dieser Gleichung zeigt folgendes Täfelchen für verschiedene Werte von i, c und z (Zenitdistanz); die Tafelwerke gelten in sehr nahe gleichem Betrage sowohl für das erste als auch für das zweite Glied der rechten Seite der Gleichung für Δ z. – Man sieht also, daß bei geringen Höhen selbst bei recht mangelhafter Justierung des Instruments der Einfluß der Instrumentfehler recht gering bleibt.

Wegen des Einflusses der Strahlenbrechung (Refraktion, s.d.) mißt man die Zenitdistanzen sowohl bei irdischen als auch cölestischen Objekten stets zu gering, die Höhen zu groß. – Im ersteren Falle hängt die Korrektion wegen Strahlenbrechung von der Distanz des anvisierten Objektes ab und ist gleich.

Δ z = (1 – k)/2R d²,

wo k im Mittel gleich 0,13, R der Erdradius (6381000 m) und d die horizontale Entfernung des Objektes vom Beobachtungsort in Metern ausgedrückt ist. Der Betrag der »astronomischen« Refraktion hängt nur von der Zenitdistanz des anvisierten Gestirnes und von dem physikalischen Zustand der Atmosphäre ab. Im Horizont beträgt sie etwa 32 Bogenminuten, bei 45° Höhe etwa 1' und im Zenit ist sie gleich Null. – Genaueres über diesen Gegenstand muß in dem Art. Refraktion nachgelesen werden. – Durch die Schwere wird sowohl das Objektiv- als auch das Okularende des Fernrohres nach unten gebogen; ist diese Biegung in den verschiedenen Zenitdistanzen verschieden, so tritt zu vorstehenden Korrektionen für Höhenwinkel noch eine solche für Biegung hinzu, welche im Horizont ihr Maximum erreicht, im übrigen aber dem Sinus der Zenitdistanz proportional ist. – Auch erleiden bei sehr großen Instrumenten die Kreise selbst solche der Biegung ähnliche Deformationen (vgl. darüber Universalinstrumente und Meridian- bezw. Vertikalkreise).

Literatur: Das Nähere über die Messung der Höhenwinkel muß in den Lehrbüchern der Geodäsie oder der sphärischen Astronomie nachgelesen werden; im besonderen sei hier verwiesen auf: Jordan, W., Handbuch der Vermessungskunde, Bd. 2, Feld- und Landmessung, 6. Aufl., bearbeitet von G. Reinhertz, Stuttgart 1904; Bohn, C., Die Landmessung, Berlin 1886, und Bauernfeind, CM., Elemente der Vermessungskunde, Stuttgart 1890. Bezüglich der astronomischen Höhenmessung sind zu vergleichen die Lehrbücher der sphärischen Astronomie von Brunnow, Chauvenet, Heer und Tinter und die Hilfstafeln für geographische Ortsbestimmungen von Th. Albrecht.

Ambronn.