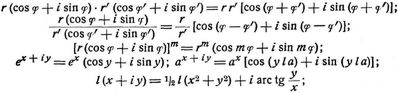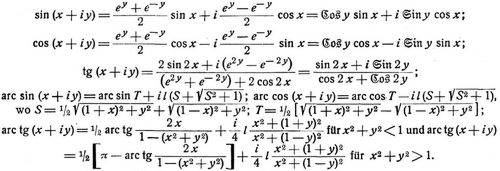- Komplexe Größen
Komplexe Größen, Summen von reellen und imaginären Größen; sie sind von der Form a + bi.
Zwei komplexe Größen sind dann und nur dann einander gleich, wenn die reellen und die imaginären Teile einzeln einander gleich sind; aus a + bi = a' + b'i folgt daher a = a'; b = b'. Zwei komplexe Größen a + bi und a – bi, die sich nur im Vorzeichen des imaginären Teils unterscheiden, heißen komplex konjugiert oder kurz konjugiert. Ihre Summe 2a und ihr Produkt a2 + b2, die sogenannte Norm, ist reell. Hat eine Gleichung mit reellen Koeffizienten eine komplexe Wurzel, so hat sie auch die zu derselben konjugierte. Eine komplexe Zahl a + bi wird geometrisch dargestellt, indem man ihr in einer Ebene (der sogenannten Gaußschen Ebene) vermittelst eines rechtwinkligen Koordinatensystems den Punkt (a, b) anordnet. Dabei bilden sich die reellen Zahlen auf der x-Achse, die rein imaginären auf der y-Achse ab. Führt man noch Polarkoordinaten ein, so heißt der Radiusvektor r = √(a2 + b2) auch absoluter Betrag oder Modul; hierzu kommt noch der Polarwinkel φ = arc tg b/a. Dabei ist a + bi = r (cos φ + i sin φ) = reiφ, wobei cos φ + i sin φ = eiφ als Richtungskoeffizient bezeichnet wird.
Jede Funktion einer komplexen Größe läßt sich auf die Form einer komplexen Größe bringen. Hierbei gelten die Formeln:
a + bi ± (a' + b'i) = a ± a' + (b ± b') i.
(Der Modul einer Summe ist nicht größer als die Summe und nicht kleiner als die Differenz der Module der Summanden; der Modul der Differenz zweier komplexen Zahlen ist gleich der Entfernung der Punkte, in die sich die Zahlen abbilden.)
[581] Literatur: Hankel, Theorie der komplexen Zahlen, Leipzig 1867.
Wölffing.
http://www.zeno.org/Lueger-1904.