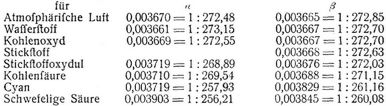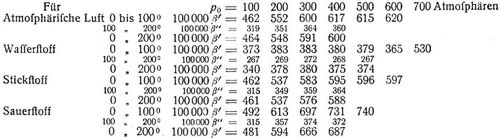Spannungskoeffizient

Spannungskoeffizient. Wirkt auf die ganze Oberfläche eines Körpers lediglich ein gleichmäßig verteilter Normaldruck und es findet bei konstantem Volumen eine Aenderung der Temperatur statt, wobei die Drücke pro Flächeneinheit p₀, p den Temperaturen 0 und t° entsprechen, so heißt

der Spannungskoeffizient bei t°. Dieser bedeutet hiernach auch annähernd die Druckänderung pro Einheit des Druckes bei 0⁰ Δ p/p₀ durch Δ t = 1° Temperaturänderung (gewöhnliche Definition).

Wird anstatt des im allgemeinen veränderlichen Spannungskoeffizienten β ein mittlerer Spannungskoeffizient β' eingeführt, der von 0 bis t die gleiche Druckänderung p – p₀ bedingt wie der variable Koeffizient β, so hat man

und wenn die Drücke p, p₁ den Temperaturen t, t₁ entsprechen und β', β'₁ die mittleren Spannungskoeffizienten von 0 bis zu diesen Temperaturen bezeichnen:

worin für β', β'₁ vielfach der gleiche Mittelwert gesetzt wird. Beziehungen zwischen dem Spannungs-, dem Ausdehnungs- und Kompressionskoeffizienten s. [4], [5], [6], S. 495, [11], S. 589, [16], S. 72.

Für Gase ist unter Voraussetzung des Boyle-Gay-Lussacschen Gesetzes (s.d.) der Spannungskoeffizient gleich dem Ausdehnungskoeffizienten (s.d.) und konstant, β = β' = α [16], S. 75, wobei oft nach Regnaults Vorschlag (Poggendorffs Annalen 1842, LV, S. 564) α = 0,003665 und noch häufiger α = 1/273 = 0,003663 gesetzt wird. Regnault selbst gibt auf Grund seiner Versuche für Anfangsspannungen nahe einer Atmosphäre folgende Mittelwerte von 0 bis 100° [3], I, S. 91:

und speziell für atmosphärische Luft [3], I, S. 110:

dagegen für die Kohlensäure [3], I, S. 112:

Wenn hiernach die Veränderlichkeit von β für die schwerstkondensierbaren Gase (zu welchen die Kohlensäure nicht gehört), bei gewöhnlichen Drücken, nicht groß ist, so treten doch auch für diese Gase bei hohen Drücken ganz andre β ein. Amagat hat Versuche bis p₀ = 280 Atmosphären angestellt ([9], S. 1041), aus welchen er u.a. folgende β' von 0 bis nahe 100° und die Werte

[159] von etwa t₁ = 100 bis t = 200° berechnete. Wir fügen die alsdann nach 2., 4. durch

1/200 [(1 + 100β') (1 + 100β'') – 1]

ausgedrückten mittleren Spannungskoeffizienten von 0 bis 200° bei (vgl. die entsprechenden Ausdehnungskoeffizienten α', Bd. 4, S. 313).

wonach der Spannungskoeffizient mit dem Drucke erheblich wächst, aber mit der Temperatur nur wenig veränderlich ist. Ueber β, β' bei Drücken von 1 bis 0,08 Atmosphären s. [8], [11], S. 130, über den Spannungskoeffizienten nach der Zustandsgleichung von van der Waals [11], S. 127, [15], S. 131.

Für Quecksilber von p₀ = 1 Atmosphäre und t = 0° ergab sich ∂ p/∂ t = 46,21 ([11], S. 595), wonach für Δ t = 1° der Druck um etwa Δ p = 46,21 Atmosphären zunehmen würde. Für Wasser hat Amagat die ∂ p/∂ t und ∂ p/p ∂ t bei Anfangsdrücken p₀ von 1 bis 896 Atmosphären und Temperaturen von 0 bis 100° und dann bei Anfangsdrücken von 1 bis 2508 Atmosphären und Temperaturen von 0 bis 48,85° in Tabellen zusammengestellt [10], S. 781. Beispielsweise fand er für p₀ = 1 Atmosphäre

Mit Rücksicht hierauf folgt aus

die bei konstantem Volumen eintretende Druckerhöhung des Wassers

von 0 bis 50°: Δp = 10 (0,27 + 3,1 + 5,8 7,9 + 10,1) = 272 Atmosphären,

von 50 bis 100°: Δp = 10 (12,3 + 12,7 + 14,3 + 15,5 + 16,6) = 714 Atmosphären,

also von 0 bis 100°: Δp = 272 + 714 = 986 Atmosphären.

Resultate für andre Flüssigkeiten s. [9], S. 1238, die ∂ p/∂ t für Gase [9], S. 1041, [13].

Für isotrope feste Körper hat man [7], [16], II, S. 380:

worin E der Elastizitätsmodul (s.d.), α der lineare Ausdehnungskoeffizient (s.d.), e der Elastizitätsquotient (s.d.). Setzt man beispielsweise für Eisen ε = 4, α = 0,000012 und pro Quadratmeter E = 20000000 t, so folgt aus 6. ∂ p/∂ t = 480, jeder Grad Temperaturerhöhung erzeugt eine Druckzunahme von etwa 480 t pro Quadratmeter oder 48 kg pro Quadratzentimeter, [7], S. 173, [16], S. 381.

Literatur: [1] Magnus, Ueber die Ausdehnung der Gase durch Wärme, Poggendorffs Annalen 1842, LV, S. 1. – [2] Regnault, Untersuchung über die Ausdehnung der Gase, ebend. 1842, LV, S. 391, 557; 1842, LVII, S. 115. – [3] Ders., Relations des expériences etc., Paris 1847 (zugleich Bd. 21 der Mémoires de l'Académie des sciences), S. 15. – [4] Zeuner, Grundzüge der mechanischen Wärmetheorie, Leipzig 1866, S. 539. – [5] Grashof, Theoretische Maschinenlehre, I, Leipzig 1875, S. 121, 123, 133. – [6] Rühlmann, Handbuch der mechanischen Wärmetheorie, I, Braunschweig 1876, S. 466. – [7] Weyrauch, Aufgaben zur Theorie elastischer Körper, Leipzig 1885, A. 66, 67, 103. – [8] Melander, Ueber die Ausdehnung der Gase bei niedrigen Drücken, Wiedemanns Annalen 1892, XLVII, S. 135. – [9] Amagat, Sur les lois de dilatation à volume constant des fluides. Coefficient de pression. Comptes rendus etc. 1892, CXV, S. 1041, 1238. – [10] Ders., Dilatation de l'eau sous pression constante et sous volume constant, Comptes rendus 1893, CXVI, S. 779 (s.a. S. 946). – [11] Wüllner, Lehrbuch der Experimentalphysik, II, Die Lehre von der Wärme, Leipzig 1896, S. 103, 122, 125, 589. – [12] Pfaundler, Müller-Pouillets Lehrbuch der Physik, 112, Von der Wärme, Braunschweig 1898, S. 107, 112, 120. – [13] Landolt-Börnsteins Physikalisch-chemische Tabellen, Berlin 1905, S. 215, 216. – [14] Chwolson, Lehrbuch der Physik, III, Die Lehre von der Wärme, Braunschweig 1905, S. 14, 138, 140, 145, 152, 441. – [15] Winkelmann, Handbuch der Physik, III, Wärme, Leipzig 1906, S. 110, 114, 116, 120, 131, 134, 472. – [16] Weyrauch, Grundriß der Wärmetheorie, I, Stuttgart 1905, S. 70, 75, 126, 129; II, Stuttgart 1907, S. 380.

Weyrauch.