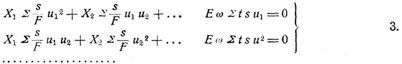- Temperaturspannungen
Temperaturspannungen in Baukonstruktionen, d. s. innere Spannungen infolge Temperaturänderungen, werden durch Aenderungen in dem Wärmezustände derselben hervorgerufen, wenn die freie Ausdehnung der ganzen Konstruktion oder einzelner Teile behindert ist. Diese Behinderung ist im allgemeinen bei[520] allen Konjunktionen vorhanden, welche in ihrer geometrischen Form überbestimmt sind, d.h. welche mehr sie zusammensetzende Teile enthalten oder mehr äußeren, die Ortsveränderung einzelner Punkte einschränkenden Bedingungen unterworfen sind, als für die Starrheit (Unverschieblichkeit) der Form oder deren Festhaltung im Räume notwendig ist. Derartige Konstruktionen sind auch statisch unbestimmt (s. Fachwerke und Träger, statisch bestimmte und unbestimmte), und es treten daher auch nur in statisch unbestimmten Systemen infolge von Temperaturänderungen innere Spannungen auf.
Denkt man sich in einem solchen Systeme die statische Unbestimmtheit (geometrische Ueberbestimmtheit), also auch die Behinderung der freien Ausdehnung, durch Weglassung von die Unverschieblichkeit nicht beeinträchtigenden Teilen (Fachwerksstäbe oder Auflagerbedingungen) beseitigt, und ersetzt man deren Wirkung durch Anbringung von vorläufig unbekannten Kräften X1 X2 ... (Spannungen, Stabkräfte oder Auflagerkräfte), so lassen sich diese Kräfte, welche durch eine Temperaturänderung des Systems um t° hervorgerufen werden, aus dem Gesetze der virtuellen Verschiebungen ableiten. Für ein Fachwerksystem sei für irgend ein Stabglied s die Länge, F die Querschnittsfläche, S die Stabkraft, t die Temperatur gegenüber einem spannungslosen Anfangszustand, ω der Wärmeausdehnungskoeffizient, 1/E der elastische Dehnungskoeffizient, dann ist die Längenänderung dieses Stabes
Δs = S s/E F + ω t s.
1.
Erzeugt ferner die an Stelle von X1 wirkend gedachte Krafteinheit in dem beliebigen Fachwerkstabe die statisch bestimmbare Spannung u, jene an Stelle von X2 wirkende Krafteinheit die Spannung u2 u.s.w., so ist nach dem obzitierten Satze für das ganze System
Σu1 Δs = 0, Σu2 Δs = 0 ...,
2.
Da aber beim Fehlen jeder äußeren Belastung S = X1 u1 + X2 u2 + ... ist, so folgen mit Einsetzung von 1. und bei durchaus gleichem Elastizitätskoeffizienten E und Ausdehnungskoeffizienten ω aus 2. die Bestimmungsgleichungen
Mit den Größen X1 X2 ..., welche aus den vorstehenden Gleichungen folgen, sind aber auch die sämtlichen inneren Kräfte S gegeben. Als Bedingung, daß die Kräfte X = 0 werden, daß sonach gar keine Spannungen infolge der Temperaturänderung auftreten, ergibt sich Σtsu1 = 0, Σtsu2 = 0 ... oder bei einem gleichmäßigen Wärmeunterschiede gegen den spannungslosen Anfangszustand
Σ s u1 = 0, Σ s u2 = 0 ...,
4.
Die Bedingung 4. kann bei manchen statisch unbestimmten Systemen erfüllt sein. In diesem Falle hat eine durchaus gleichmäßige Erhöhung oder Erniedrigung der Temperatur keine inneren Spannungen zur Folge. Beispiele: der kontinuierliche Balkenträger, der Bogenträger mit Horizontalzugband, das aus dem Viereck mit gekreuzten Diagonalen bestehende Fachwerkselement u.a. Ungleiche Erwärmungen bewirken jedoch auch bei diesen Systemen innere Spannungen.
Die Berücksichtigung der Temperaturspannungen ist namentlich bei jenen Systemen von Wichtigkeit, bei welchen auch gleichmäßige Veränderungen der Temperatur einen Einfluß üben. Es sind dies insbesondere die statisch unbestimmten Bogen- und Hängeträger. Bei der Ermittlung der durch die Temperaturänderung in metallischen Konstruktionen hervorgerufenen Spannungen pflegt man für unsre klimatischen Verhältnisse mit der Annahme zu rechnen, daß Temperaturen zwischen –25° und +45° vorkommen, daß sonach, eine mittlere Aufstellungstemperatur von +10° vorausgesetzt, die Wärmeschwankungen in freistehenden eisernen Bauwerken (Brücken) ±35° C. betragen. Ist das Bauwerk in einzelnen Teilen gegen die unmittelbare Sonnenbestrahlung geschützt, so kann nach diesbezüglichen Beobachtungen der Temperaturunterschied zwischen den wärmsten und kältesten Stellen einer Eisenkonstruktion an sonnigen Tagen bis 14° C. erreichen. Bei Steinbauten, namentlich solchen von stärkeren Abmessungen, werden so große Wärmeschwankungen wie bei metallischen Konstruktionen im allgemeinen nicht vorkommen, da stärkeres Mauerwerk sich im Sommer kaum auf die höchste Lufttemperatur erwärmen und anderseits auch bei einiger Zeit anhaltendem Froste nicht auf die tiefste Lufttemperatur abkühlen wird. Für Brückengewölbe wird es ausreichen, eine Wärmeschwankung von ±20° oder von +15° und –25° zugrunde zu legen.
Melan.
http://www.zeno.org/Lueger-1904.