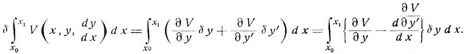Variationsrechnung

Variationsrechnung, die Lehre über Maxima und Minima von Integralen, indem Funktionen gesucht werden der Art, daß gewisse Integrale einen größten oder kleinsten Wert annehmen.

Als Variationen bezeichnet man die Aenderungen, welche die Veränderlichen, Funktionen, Integrale u.s.w. erleiden, wenn an Stelle der gesuchten Funktionen, welche den Zusammenhang der abhängigen Veränderlichen von den unabhängigen angeben, andre unendlich wenig von ihnen verschiedene Funktionen treten. Es soll z.B. y als Funktion von x derart bestimmt[745] werden, daß das Integral

zu einem Maximum oder Minimum wird. Dabei ist V eine gegebene Funktion von x, y und d y/d x = y' Die Variation des Integrals ist

Hier sind δ y und δ y' die Variationen von y und y'. Soll das Integral ein Maximum oder Minimum sein, so muß

sein, wodurch sich y in Funktion von x bestimmt. Sind die Grenzen x₀ und x₁ sowie die zugehörigen Werte y₀ und y₁ nicht konstant, so treten hierzu noch gewisse Grenzbedingungen. Nach Poisson kann man die Untersuchung der letzteren umgehen, indem man nach Bestimmung von y in Funktion von x die Aufgabe als gewöhnliches Maximum- oder Minimumproblem weiter behandelt und hierdurch die Integrationskonstanten bestimmt. Bei den isoperimetrischen Problemen ist noch eine Nebenbedingung in Gestalt eines bestimmten Integrals zwischen denselben Grenzen

gegeben. Alsdann ist in die Gleichung

an Stelle von V die Funktion V + λ V₁ einzusetzen. λ ist dabei eine Konstante, die sich später aus der Nebenbedingung bestimmt. Liegen mehrere abhängige Veränderliche vor, so daß

zu einem Maximum oder Minimum zu machen ist, so hat man zur Bestimmung von y, z ... die Gleichungen

Besteht hierbei noch eine Nebenbedingung in Gestalt einer gewöhnlichen oder Differentialgleichung V₁ (x y y' z z' ...) = 0, so ist an Stelle von V zu setzen V + λ V₁. In diesem Falle in k nicht eine Konstante, sondern eine Funktion von x. Kommen in V höhere Ableitungen y'' y''' ... vor, so bestimmt sich y aus:

Kommen in V außer der abhängigen Veränderlichen z noch zwei unabhängige x und y vor und das Integral ist ein Doppelintegral nach x und y:

so ergibt sich z aus:

Die zweite Variation gibt Aufschluß, ob Maximum oder Minimum vorliegt,

Literatur: [1] Moigno-Lindelöf, Calcul des variations, Paris 1861. – [2] Jellet, J.H., Grundlehren der Variationsrechnung, bearbeitet von Schnuse, Braunschweig 1860. – [3] Todhunter, Researches in the calculus of variations, London 1871. – [4] Dienger, Grundriß der Variationsrechnung, Braunschweig 1867. – [5] Abhandlungen über Variationsrechnung (Verfasser: Johann und Jakob Bernouilli, Euler, Lagrange, Legendre, Jacobi), herausgegeben von P. Stäckel, Bd. 1 und 2, Leipzig 1894. – [6] Zermelo, Untersuchungen zur Variationsrechnung Diss., Berlin 1894. – [7] Carll, L.B., Treatise on the calculus of variations, London 1885. – [8] Kneser, A., Lehrbuch der Variationsrechnung, Braunschweig 1900. – [9] Pascal, E., Die Variationsrechnung, deutsch von Schöpp, Leipzig 1899. – [10] Bolza, O., Vorlesungen über Variationsrechnung, I, Leipzig 1908.

Wölffing.