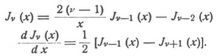- Besselsche Funktionen
Besselsche Funktionen, auch Zylinderfunktionen genannt, von Bessel bei astronomischen Untersuchungen benutzt, sind Funktionen zweier veränderlichen Größen x und ν, die der u.a. auch bei verschiedenen Problemen der mathematischen Physik auftretenden sogenannten Besselschen Differentialgleichung:
genügen. (Ueber deren vollständige Integration s. unten.)
Die Besselsche Funktion erster Art Jn (x) oder Jn (x) läßt sich durch die für jeden (reellen oder komplexen) endlichen Wert von x und ν konvergente unendliche Reihe
definieren, worin Γ das Zeichen der Gammafunktion (s.d.) ist. Von ihren zahlreichen Eigenschaften seien erwähnt:
Die vollständige Lösung der Besselschen Differentialgleichung lautet im allgemeinen
y = A Jν (x) + B J-ν(x)
mit A und B als willkürlichen Konstanten. Ist jedoch ν eine (positive oder negative) ganze Zahl oder Null, etwa ν = n, so wird
J+n(x) = (- 1)n J-n(x)
und die vorstehende Lösung hört auf, die allgemeinste zu sein, weil sie dann bloß eine einzige Integrationskonstante (A ± B) enthält. Man hat deshalb noch eine Besselsche Funktion zweiter Art Yn(x) oder Yn(x) eingeführt, die als Grenzwert des Ausdrucks
für ν = n erklärt werden kann und mit deren Hilfe die vollständige Lösung der Besselschen Differentialgleichung in dem fraglichen Fall sich durch
y = A Jn(x) + B Yn(x)
darstellen läßt. Man begegnet auch andern Formen der Besselschen Funktion zweiter Art, z.B. der Funktion On(x) in [1]. Von den durch Bessel und in weiterem Umfang durch Hansen berechneten Tafeln der Besselschen Funktionen erster Art findet man Abdrücke in [2] und [3]. (Bei Benutzung der Tafeln in [2], S. 158–165, ist zu beachten, daß Schlömilch mit Hansen Jn(x/2) statt Jn (x) schreibt. Die Besselschen Funktionen können als Grenzfälle der Kugelfunktionen angesehen werden [1], [4].
Literatur: [1] Neumann, C., Theorie der Besselschen Funktionen, ein Analogon zur Theorie der Kugelfunktionen, Leipzig 1867. – [2] Schlömilch, O., Ueber die Besselsche Funktion, Schlömilchs Zeitschr. f. Mathem. u. Physik., 2, Jahrg., 1857. – [3] Lommel, E., Studien über die Besselschen Funktionen, Leipzig 1868. – [4] Heine, E., Handbuch der Kugelfunktionen und der verwandten Funktionen, 2. Aufl., Berlin 1878–81, namentlich Teil I, §§ 42, 43. – [5] Todhunter, An elementary treatise on Laplace's functions, Lamés functions and Bessel functions, London 1875, Macmillan & Co. – [6] Nielsen, Niels, Handbuch der Theorie der Zylinderfunktionen, Leipzig 1904.
Mehmke.
http://www.zeno.org/Lueger-1904.