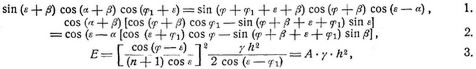- Erddruck
Erddruck ist der gegen eine beliebig gerichtete und geformte Mauerfläche ausgeübte Druck der Hinterfüllungserde. Seine Bestimmung ist nur unter gewissen Voraussetzungen theoretisch durchführbar [15].
Es sind seither drei Theorien aufgestellt worden. Die erste, ältere Theorie läßt sich nach Winkler ([4], S. 59) ihrem Ursprung nach auf das Ende des 17. Jahrhunderts zurückführen (Vauban 1687, Bullet 1691) und nimmt an, daß von der gestützten Erdmasse beim Nachgeben der Mauer sich ein Erdprisma loslöst, dessen Gewicht, entsprechend zerlegt, den Erddruck ergibt. Durch Coulomb (1773) erfuhr diese Theorie eine weitere Ausbildung, indem durch ihn der Begriff des »Erdprismas vom größten Druck oder Schub« eingeführt wurde, auf Grund welcher Anschauung namentlich Prony [4], S. 65, François [4], S. 66, Navier [4], S. 68, Poncelet [4], S. 72 und 78, Hagen [4], S. 74, Scheffler [4], S. 84, Culmann [l], Rebhann [2], Wittmann [6] und Weyrauch [7] diese Theorie nach verschiedenen Richtungen für die Praxis nutzbar machten. – Die zweite neuere Theorie flammt erst aus der zweiten Hälfte des 19. Jahrhunderts und haben sich im wesentlichen Rankine (1856) [4], S. 102, [7], S. 204, Scheffler (1851) [4], S. 100, Lévy (1867) [4], S. 104, Considère (1870) [4], S. 105, Mohr (1871) [3] und [4], S. 107, Winkler (1872) [4], Weyrauch [11] und Häseler [12] um sie verdient gemacht. Die neuere Theorie geht, ganz wie die Elastizitäts- und Festigkeitslehre, von der Untersuchung des Gleichgewichtes der Erdelemente im unbegrenzten Erdkörper aus und setzt an Stelle des Elastizitätsgesetzes das Gesetz der Reibung und Kohäsion. – Eine dritte Theorie endlich hat Engesser [10] aufgestellt, indem er die homogene Erdmasse durch ein starres Keilsystem ersetzt denkt und auf graphischem Wege zur Bestimmung der Größe und Richtung des Erddruckes gelangt. Dabei wird die Annahme der Bildung eines kleinstmöglichen Horizontalschubes in dem seinem eignen Gewicht überlassenen Erdkörper gemacht. Seine Ergebnisse stimmen im wesentlichen mit denen Winklers überein. Die beiden neueren Theorien finden in der Praxis selten Anwendung, und wenn auch in gewissen Fällen, z.B. bei Bestimmung des Erddrucks gegen schiefe Flügelmauern, nur die zweite Theorie anwendbar erscheint, so genügt in den meisten Fällen der Praxis die Anwendung der älteren Theorie, besonders da die sorgfältigen neueren Versuche von Siégler [13] und Donath [14] in der Erläuterungsweise von Engesser dargelegt haben, daß der Erddruck gegen lotrechte Wände unter dem Reibungswinkel φ gegen die Wandnormale geneigt ist [15], S. 326, und seine Größe genügend genau nach der älteren Theorie von Coulomb bestimmt werden kann.
Im nachstehenden soll hauptsächlich die ältere Theorie besprochen und die Anwendung der analytischen Formeln mitgeteilt werden. Dabei wird die Erde kohäsionslos und die Bruchfläche eben angenommen. Erstere Annahme entspricht der für die Stützmauer ungünstigsten Belastung, da die Berücksichtigung der Kohäsion einen kleineren Eindruck zur Folge haben müßte; auch ist frisch angeschüttete Erde fast stets kohäsionslos, und die notwendigerweise zu berücksichtigende Reibung kann nicht gleichzeitig mit der Kohäsion auftreten, sondern erst, nachdem diese überwunden ist [4], S. 98, [10], S. 189, [8], S. 529, [12], S. 296. Die zweite Annahme, daß die Bruchfläche eben und nicht gekrümmt ist, hat sich für die Praxis als genügend genau herausgestellt und wird dies u.a. durch die Versuche von Cramer [9] bestätigt.
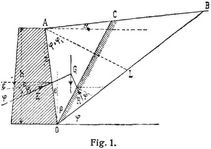
Bezeichnet in Fig. 1 O C die Lage der als eben vorausgesetzten Bruchfläche, also Dreieck O A C die Grundfläche eines größten Bruchprismas, dessen Höhe gleich 1 angenommen werden soll, so wird sein im Schwerpunkt des Bruchprismas angreifendes Gewicht G (= A C O · 1 · y) sich in zwei Kräfte E und R zerlegen lassen, die unter den Reibungswinkeln φ1 bezw. φ zu den Senkrechten der Flächen A O bezw. O C wirken werden. Sobald also die Richtung der Trennungsfläche O C und der Winkel φ1 bekannt sind, läßt sich die Richtung und Größe des Erddrucks E mit Hilfe des Kräftepolygons konstruieren oder aus den Gleichgewichtsbedingungen berechnen, da Winkel φ als natürlicher Böschungswinkel (s. Reibungswinkel) für das betreffende Erdmaterial und die Lage O A der hinteren Mauerfläche als gegeben betrachtet werden muß.
Der Reibungswinkel φ1 des Erddrucks E mit der Mauerfläche wurde von Coulomb gleich Null gesetzt. Seit Poncelet (1840) nehmen viele Autoren (Häseler [12], S. 309, Wittmann [6], S. 59, u.s.w.) ihn gleich dem Reibungswinkel φ von Erde auf Erde, während andre (Mohr [3], S. 364, Weyrauch [7], S. 206, Schäffer [8], S. 535), ihn veränderlich und als aus den jedesmaligen Gleichgewichtsbedingungen zu berechnende Größe ansehen. Danach kann der Winkel φ1 bei Vernachlässigung der Kohäsion, alle Werte von φ1 = 0 bis φ1 = ± φ, und zwar letztere nur dann annehmen, wenn die Lage der Mauerfläche OA mit einer »Gleitfläche« des Erdkörpers zusammenfällt.
Analytisch findet man die Größe des Erddrucks E und dessen Richtung φ1 gegen die Senkrechte auf A O durch Aufstellung von sechs Bedingungsgleichungen [8], S. 537: 1. die Komponenten parallel zu O C = 0, 2. die Komponenten senkrecht zu O C = 0, 3. die Summe der Momente = 0, 4. die durch Differentiation erhaltene Gleichung, durch welche die Gleitfläche für das Erdprisma vom größten Druck festgestellt wird, 5. und 6. die Momentengleichungen des Erddrucks E und der Seitenkraft R um O als Resultierende sämtlicher parallel zueinander gedachten Elementardrucke. Auf diesem Wege findet man nach Weyrauch [7] mit Bezug auf die Fig. 1 folgende Beziehungen, die hinreichen, um den Winkel φ1, die Neigung der Gleitfläche ß und die Größe des Erddrucks für gewisse Fälle zu berechnen:
[477] worin γ das Gewicht der Kubikeinheit Erde und
Für α = 0, d.h. für horizontal abgeglichene Erdoberfläche AB wird Gleichung 1. nach verschiedenen Umformungen:
Diese Gleichung ist erfüllt für 2 ß + φ = 90°, also ß = 90 – φ/2 d.h. die Gleitfläche oder Bruchfläche halbiert in diesem Fall den Winkel zwischen der Lotrechten und der natürlichen Böschung. Hierbei wird:
Für den Reibungswinkel φ1 ergibt sich in diesem Fall:
oder in bequemerer Form für die Richtung des Erddrucks gegen den Horizont
Für α = φ, d.h. für ein unter dem natürlichen Böschungswinkel anzeigendes Gelände ergibt sich aus 1. und 2.:
Diese Gleichung ist erfüllt für ß = 90 – φ, d.h. für ein unter dem natürlichen Böschungswinkel ansteigendes Gelände fällt die Bruchfläche mit der natürlichen Böschungsfläche zusammen. Die Schnittpunkte B und C liegen im Unendlichen der natürlichen Böschung O B. Ferner wird n = 0, also:
Für den Reibungswinkel φ1 findet man
oder:
d.h. nur dann ist φ1 = φ, wenn α = φ und ε = 0, d.h. wenn die Wandfläche lotrecht steht bei unter natürlichem Böschungswinkel anzeigendem Gelände, und nur dann φ1 = 0, wenn unter der gleichen Voraussetzung für die Geländefläche die Wandfläche mit der letzteren den Winkel ε = 45 + φ/2 einschließt.
Ist der Winkel φ1 für einen vorliegenden Fall bestimmt oder hat man über ihn verfügt, so kann auch das weniger umständliche und für die Praxis genügend genaue graphische Verfahren (s.d. folg. Art.) eingeschlagen werden.
Ist die obere Begrenzungsfläche keine Ebene, also die Linie A B eine wellenförmige oder gebrochene, so können nur Näherungswerte erhalten werden, indem man die Begrenzung in eine Gerade verwandelt und für diese die Bestimmung vornimmt [6], S. 59, [8], S. 535, [12], S. 301, [16], S. 212. Findet eine gleichmäßige Belastung der oberen Begrenzungsfläche mit p für den Meter statt, so ist zu der Größe des Erdprismengewichtes γ Δ O A C das Gewicht p · A C hinzuzuaddieren, um dafür den Erddruck zu finden. In den analytischen Formeln ist für γ die Größe
einzusetzen [8], S. 535, [16], S. 201. Bei hinterschnittenen, hinten überfallenden Mauern werden alle Theorien unsicher [8], S. 538, [7], S. 205. Desgleichen wenn gleichzeitig Erschütterungen unter dem Einfluß von Betriebslasten auftreten, wie dies bei Eisenbahndämmen der Fall ist. Hier empfiehlt es sich, bei Mauern ohne Ueberschüttung den Erddruck senkrecht zur Stützwand anzunehmen, während bei Mauern mit sehr hoher Ueberschüttung die Coulombsche Theorie angewendet werden kann [15], S. 326.
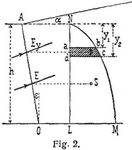
Den Angriffspunkt des Erddrucks E erhält man [4], S. 49, [8], S. 534, [12], S. 313, [16], S. 209, wenn für jeden Höhenabschnitt y (s. Fig. 2) die Größe des an dieser Stelle auf die Flächeneinheit wirkenden Erddrucks Ey als Ordinate von N L aus wagerecht aufgetragen wird, in der Höhenlage des Schwerpunktes S der zwischen der so entstandenen Kurve M N und der zugehörigen Abszissenachse N L befindlichen Druckfläche L N M, weil nach der Konstruktion der Inhalt eines jeden zwischen Kurve und N L gelegenen Flächenelementes a b c d den zur betreffenden Höhenlage y2 – y1 gehörigen Erddruck Ey und, sein Schwerpunkt s' die Höhenlage des Angriffspunktes von Ey ergibt. Analytisch läßt sich die Lage des Angriffspunktes aus der Momentengleichung:
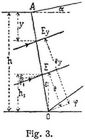
[478] (s. Fig. 3) ableiten. Für ebene Erdoberfläche ist nach Gleichung 3.: E = A γ h2, also Ey = A · γ · y2, folglich d Ey = 2 γ Ay dy. Ferner ist aus Fig. 3:
also:
somit
und die Höhe über dem Fußpunkt 0 ist
Die neuere Literatur s. unter [17]. Vgl. a. die graphische Berechnung.
Literatur: [1] Culmann, Die graphische Statik, Zürich 1866, S. 547. – [2] Rebhann, Theorie des Erddrucks und der Futtermauern, Wien 1871. – [3] Mohr, Beitrag zur Theorie des Erddrucks, Zeitschr. d. Arch. – u. Ing.-Vereins zu Hannover 1871, S. 344, und 1872, S. 67 u. 245. – [4] Winkler, Neue Theorie des Erddrucks nebst einer Geschichte der Theorie des Erddrucks und der hierüber angestellten Versuche, Wien 1872. – [5] v. Ott, Vorträge über Baumechanik, Prag 1877, S. 20. – [6] Wittmann, Geometrische Erddrucktheorie u.s.w., Zeitschr. f. Bauk. 1878, S. 53, auch in »Statik der Baukonstruktionen«, Berlin 1879, Teil 1, S. 17. – [7] Weyrauch, Zur Theorie des Erddrucks, Zeitschr. f. Bauk. 1878, S. 193. – [8] Schäffer, Erddruck und Stützwände, Zeitschr. f. Bauw. 1878, S. 527. – [9] Cramer, Erddruck und Stützwände, Zeitschr. f. Bauw. 1879, S. 521. – [10] Engesser, Geometrische Erddrucktheorie, Zeitschr. f. Bauw. 1880, S. 189. – [11] Weyrauch, Theorie des Erddrucks auf Grund der neueren Anschauungen, Wien 1881, auch Allgem. Bauztg. 1880., S. 63 u. 77. – [12] Häseler, Handb. d. Ingen.-Wissensch., Teil I, Bd. 2, 4. Aufl., Leipzig 1905, Kap. 3. – [13] Siegler, Ann. des ponts et chaussées 1887, Bd. 1, S. 488. – [14] Donath, Zeitschr. f. Bauw. 1891, S. 491. – [15] Engesser, Neuere Versuche über die Richtung und Größe des Erddrucks gegen Stützwände, Deutsche Bauztg. 1893, S. 325. – [16] Löwe, Straßenbaukunde, Wiesbaden 1895, S. 201. – [17] Ueber Erddruck und Stützmauern, Zentralbl. d. Bauverw. 1896, S. 134, 150, 178, 314, 354, 497; Engels, Zur Frage der Richtung des Erddruckes auf Stützmauern, ebend. 1897, S. 144; Beyershaus, Ueber die Richtung des Erddruckes auf Futtermauern und Bohlwände, ebend. 1900, S. 234 und 263; H. Müller-Breslau, Ueber die Messung der Größe und Lage unbekannter Kräfte (Winddruck, Erddruck), die auf ruhende Körper wirken, ebend. 1904, S. 366; Francke, A., Einiges über Erddruck, Zeitschr. f. Arch. u. Ingenieurw. 1905, S. 295.
L. v. Willmann.
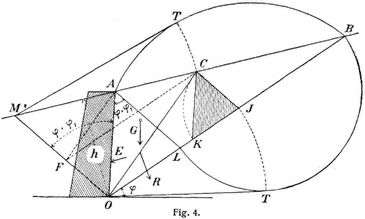
Graphische Berechnung. Wenn sich (Fig. 4) die hinter einer Stützmauer befindliche Erde längs der Bruch- oder Gleitfläche O C löst und keilartig wirkend die Mauer nach vorn schiebt, so zerlegt sich das Gewicht G des prismatischen Erdkörpers O A C in zwei Seitenkräfte R und E, von denen erstere mit O C den Winkel 90-φ, letztere mit O A den Winkel 90–φ1 einschließt. (Bezüglich der Wahl der Winkel φ und φ1 s. unten.) Dreht man das Kräftepolygon G R E um 90–φ nach rechts, so wird G | O B, R | O C und E parallel zu einer Linie O M, die mit O A den Winkel φ + φ1 einschließt. Zieht man C J || Q M, so ist das Dreieck O C J dem Kräftepolygon ähnlich. Es verhält sich E : G = C J : O J. Ferner ist G = 1/2 γ/h · A C, wenn y das spezifische Gewicht der Erde bedeutet, folglich: E = 1/2 γ h A C · C J/O J.
Bei sich ändernder Bruchfläche bleiben γ und h unverändert, während A C, C J und O J sich ändern. Dabei ist C J proportional C B und O J proportional M C. Der Erddruck wird daher am größten, wenn der Ausdruck A C · C B : M C sein Maximum erreicht. Setzt man M C = x, so wird dieser Ausdruck gleich (x – M A)(M B – x) : x und sein größter Wert ergibt sich für
Man zeichnet über AB einen Kreisbogen, legt aus M eine Tangente daran und dreht diese herum nach M C, so ist O C die ungünstigste Bruchfläche.
Zu demselben Ziele gelangt man offenbar auch, wenn man AL || M O zieht, über B L einen Kreisbogen zeichnet, aus O die Tangente daran legt und deren Länge nach O J herumdreht. Zieht man (s. Fig. 4) A F || O C, so verhält sich M F : M O = M A : M C = M C : M B, folglich ist F C O B. Daraus folgt Δ O A C = Δ O F C = Δ O C J, d.h. die ungünstigste Bruchfläche halbiert das Viereck O A C J. Nach dem Früheren verhält sich der Erddruck E zum Gewichte G des abgleitenden Erddreiecks wie C J zu O J. Macht man J K = J C, so ist demnach der Erddruck E = γ · Δ C J K. Um möglichst rasch zu dem Dreiecke C J K zu gelangen, zieht man die natürliche Böschung O B und die Linie A L unter dem Winkel φ + φ1 zu A O. Hierauf bestimmt man mittels eines Kreisbogens O J als mittlere Proportionale von O B und O L, zieht J C L A und macht J K = J C Diese übersichtliche Darstellung des Erddrucks ist zuerst auf etwas anderm Wege von Rebhann abgeleitet worden.
Fällt (Fig. 4) die Erdoberfläche A B nach rechts um den Winkel φ1, so ist < A B O gleich < O A L = φ + φ1. Folglich J A B O ~ J O A L. Es verhält sich somit O B : O A = O A : O L, woraus folgt O A = O J. Da die Gleitfläche das Viereck O A C J halbiert, so halbiert sie in[479] diesem Falle auch den Winkel A O B. – Dasselbe ist der Fall bei wagerecht abgeglichener Erde, wenn der Winkel φ1 = 0 gesetzt wird, wie dies der Sicherheit wegen in der Praxis sehr oft geschieht. – Läuft die Erdoberfläche parallel zur natürlichen Böschung, so rückt der Punkt C ins Unendliche, die Gleitfläche fällt mit der natürlichen Böschung zusammen und die feste C J des Erddruckdreiecks wird gleich A L (Fig. 4).
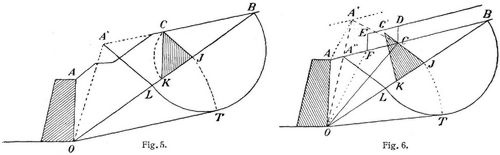
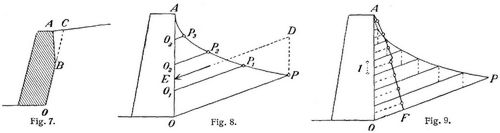
Bei überhöhtem Erdkörper (Fig. 5) verwandelt man das Vieleck O A C B in ein Dreieck O A' B von gleichem Flächeninhalt (s. Verwandlung von Flächen). Dann zieht man A'L unter dem Winkel φ + φ1 zu AO und verfährt wie vorher. – Bei belastetem Erdkörper (Fig. 6) trägt man die Belastung, auf Erde verwandelt, als Parallelstreifen auf, zieht in doppelter Streifenhöhe eine Parallele zu A B und macht AA' || OF. Dann ist das abgleitende Sechseck O A F E D C gleich dem Dreieck O A' C, in welchem A' ein von der Gleitfläche unabhängiger Punkt ist. Die abgleitende Erdmasse ist daher proportional der Strecke A'' C. Zieht man noch A'' L unter dem Winkel φ + φ1 zu O A, so ist auch dieser Fall auf den ersten zurückgeführt. Nur muß das Druckdreieck im Verhältnis O A'' zu O A' vergrößert werden, was durch Parallellinien leicht geschehen kann. Der Erddruck ist dann gleich y · ΔC' J K. – Bei geknickter Mauerwand (Fig. 7) bestimmt man dreierlei Erddrücke, nämlich die Drücke auf die drei Wände OC, BC und BA, und führt die zweite von den drei Kräften mit umgekehrtem Zeichen ein. – Die im Erdkörper wirkende Kohäsion wird bei der Bestimmung des Erddruckes meistens vernachlässigt.
Um den Angriffspunkt des Erddrucks zu finden, bestimmt man im allgemeinen den Druck für verschiedene Mauerhöhen A O, A O1 A O2 u.s.w. (Fig. 8), trägt das Ergebnis jeweils am unteren Ende als Linie auf und verbindet die Endpunkte P dieser Linien durch eine stetige Kurve. Das sich ergebende krummlinige Dreieck O A P verwandelt man in ein Parallelogramm O E D P von gleichem Flächeninhalt; dann ist E der gesuchte Angriffspunkt. In dem gewöhnlichsten Falle, wo der Erdkörper hinter der Mauer weder überhöht noch belastet ist, wird AP eine Parabel mit AO als Tangente, und der Angriffspunkt des Erddrucks fällt genau in den unteren Drittelpunkt der Mauerwand.
Um den Erddruck auf die Flächeneinheit, den spezifischen Erddruck, zu finden, teilt man (Fig. 9) die Mauerwand in Teile gleich der Längeneinheit, zieht durch die Teilpunkte Parallelen zu OP und trägt die Unterschiede der aufeinander folgenden Kräfte jeweilen in der Mitte der einzelnen Mauerteile auf. Die Endpunkte dieser Kräfte ergeben die Kurve A F des spezifischen Erddrucks. Wenn der Erdkörper hinter der Mauer weder überhöht noch belastet ist, wird A F eine gerade Linie.
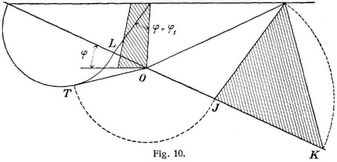
Der im bisherigen besprochene Erddruck heißt aktiver Erddruck. Er tritt auf, wenn die Mauer das Bestreben hat, nachzugeben. Wirkt jedoch umgekehrt die Mauer gegen die[480] Erde und hat letztere das Bestreben, zurückzuweichen, so geht der aktive Erddruck in den passiven über. Der passive Erddruck wird dadurch gefunden, daß man die Winkel φ und φ1 mit negativem Zeichen aufträgt. Man zieht (Fig. 10) die natürliche Böschung O B und die Linie A L nach links statt nach rechts, zeichnet über B L einen Kreisbogen, legt aus O die Tangente daran, dreht diese nach O J herüber, zieht sodann J C || A L und macht J K gleich J C, so ist der Erddruck E = γ · Δ C J K.
Bei Stützmauern kommt ausschließlich der aktive Erddruck in Betracht. Auch bei der Häuschen Untersuchung von Brückenwiderlagern, Durchlässen, Tunnelgewölben u.s.w. wird man in der Regel mit dem aktiven Drucke rechnen, wenngleich der Druck hier größer werden und dem passiven Drucke sich nähern kann.
Als Durchschnittswerte von γ und φ können folgende Zahlen angenommen werden:
Es empfiehlt sich der größeren Sicherheit wegen, den Reibungswinkel φ1 zwischen Erde und Mauer, der sehr von der Feuchtigkeit und der Beschaffenheit der Mauerfläche abhängt, gleich Null zu setzen.
Literatur: [1] Winkler, Neue Theorie des Erddrucks u.s.w., Wien 1872. – [2] Wittmann, Geometrische Erddrucktheorie u.s.w., Zeitschr. f. Bauk. 1878, auch Statik der Baukonstruktionen, Berlin 1879.
(Ritter) Mörsch.
http://www.zeno.org/Lueger-1904.