Geschwindigkeitsdiagramme

Geschwindigkeitsdiagramme. Die graphische Darstellung der Beziehung, die bei der Bewegung eines Punktes zwischen seiner Geschwindigkeit und der Zeit seiner Bewegung oder zwischen seiner Geschwindigkeit und dem durchlaufenen Weg besteht, wird ein Geschwindigkeitsdiagramm genannt.

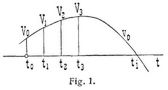
Wird in Fig. 1 die Zeit als Abszisse von einem Anfangspunkt t₀ auf eine Gerade t₀t, die Zeitachse heißt, aufgetragen, repräsentieren die gleichen Strecken t₀ t₁, t₁ t₂, t₂ t₃ ... Zeiteinheiten, z.B. Sekunden, und stellen die rechtwinkligen Ordinaten t₀ V₀, t₁ V₁, t₂ V₂, t₃ V₃ ... die Geschwindigkeiten dar, die ein bewegter Punkt bezw. nach Ablauf von 0, 1, 2, 3 ... Zeiteinheiten besitzt, dann heißt die durch die Punkte V₀, V₁, V₂, V₃ ... bestimmte Kurve v₀ das orthogonale [432] zeitliche Geschwindigkeitsdiagramm des bewegten Punktes, welches auch Geschwindigkeitskurve (s. Geradlinige Bewegung) genannt wird. Bewegt sich der Punkt von einer bestimmten Zeit t_i an entgegengesetzt, dann sind die Geschwindigkeiten von dieser Zeit an in entgegengesetztem Sinn anzutragen.

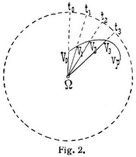
Werden die Zeiteinheiten, z.B. Sekunden, in Fig. 2 durch die gleichen Winkel t⁰Ωt₁, t₁Ωt₂, t₂Ωt₃ ... repräsentiert und die entsprechenden Geschwindigkeiten, die ein bewegter Punkt nach Ablauf von 0, 1, 2, 3 ... Zeiteinheiten besitzt, als Fahrstrahlen ΩV₀, ΩV₁, ΩV₂, ΩV₃ ... aufgetragen, dann heißt die durch die Punkte V₀, V₁, V₂, V₃ ... bestimmte Kurve V_p das polare zeitliche Geschwindigkeitsdiagramm des bewegten Punktes.

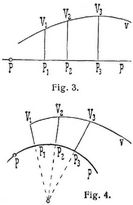
Nehmen wir an, ein Punkt P bewegt sich in Fig. 3 auf einer Geraden p, und tragen wir die Geschwindigkeiten, die der Punkt P an den Stellen P₁, P₂, P₃ ... besitzt, als rechtwinklige Ordinaten P₁V₁, P₂V₂, P₃V₃ ... auf, dann heißt die durch die Punkte V₁, V₂, V₃ ... bestimmte Kurve v das örtliche Geschwindigkeitsdiagramm des bewegten Punktes P. Nimmt dieser Punkt eine entgegengesetzte Bewegung an, dann sind auch die Geschwindigkeiten als Ordinaten im entgegengesetzten Sinn anzutragen. Bewegt sich in Fig. 4 ein Punkt P auf einem Kreise p und werden die Geschwindigkeiten, die der Punkt P an den Stellen P₁, P₂, P₃ ... besitzt, als Strecken P₁ V₁, P₂ V₂, P₃ V₃ ... von dem Kreise p angetragen, z.B. nach außen, wenn der Punkt P sich im Sinne PP₁ nach innen, wenn derselbe sich entgegengesetzt bewegt, dann erhalten wir durch die Punkte V₁, V₂, V₃ ... ein örtliches Geschwindigkeitsdiagramm v für den kreisförmig bewegten Punkt P.

Burmester.

Fig. 1.

Fig. 2.

Fig. 3., Fig. 4.