- Kugelprüfung
Kugelprüfung. Die Prüfung der Gußstahlkugeln für Kugellager erstreckt sich auf die Bestimmung der Fehlerfreiheit der Oberfläche, der Abmessungen und der Fertigkeit.
Die Untersuchung der Oberfläche erfolgt am besten mittels binokularen stereoskopischen Mikroskopes. Besonders wenn man die Kugel zuvor etwas anhaucht [1], lassen sich trotz der wirr verlaufenden Schleif- und Polierriffe etwa vorhandene Poren, Härterisse und Vertiefungen leicht erkennen.
Die Bestimmung der Abmessungen ist von besonderer Wichtigkeit, da die Güte der Kugellager wesentlich abhängt sowohl von der Uebereinstimmung der Durchmesser verschiedener Kugeln derselben Sorte als auch von den Unterschieden der Durchmesser derselben Kugel, der Unrundung. Nach Versuchen von Rasch, der die Kugeldurchmesser auf 1/1000 mm mit dem Abbeschen Dickenmesser von Zeiß bestimmte [1], ist die Genauigkeit von 1/500 mm leicht erreichbar.
Die Ermittlung der Festigkeitseigenschaften erfolgt entsprechend der Beanspruchung der Kugeln im Lager durch Druckversuche. Die einzelnen Kugeln hierbei zwischen gehärteten, ebenen Druckplatten zu belasten, ist unzulässig, da die Kugel sich eindrückt und, wenn sie überhaupt zum Bruch gebracht werden kann, nun ein zu hoher Wert für ihre Festigkeit gefunden wird. Die Druckversuche werden daher wohl allgemein nach dem Verfahren von Hertz [2]–[4] durch Gegeneinanderpressen von Kugeln derselben Sorte gleichen Durchmessers ausgeführt.
Unter der Voraussetzung, daß: 1. die Körper sich nur in kleinen Teilen ihrer Oberfläche berühren; 2. nur Kräfte senkrecht zur Oberfläche zwischen den sich berührenden Teilen wirken; 3. die Materialien der Kugeln Proportionalitätsgrenzen besitzen und diese beim Belasten nicht überschritten werden, und 4. die Kugeln homogen sind, gelten nach Hertz folgende Gleichungen:
In ihnen bedeuten: δ/2 die Annäherung von zwei benachbarten Kugeln von dem Halbmesser ρ1 und ρ2 oder die gesamte Verdrückung beider Kugeln an ihrer Berührungsstelle unter der Belastung P, r den Halbmesser der Druckfläche, ϑ1 und ϑ2 Elastizitätskoeffizienten des Materials der Kugeln. Hierbei besteht zwischen & einerseits und der Dehnungszahl α = 1/E sowie dem Verhältnis μ zwischen Querzusammenziehung und Längsdehnung anderseits die Beziehung: ϑ = 4 α (1 – μ2). Setzt man μ = 3/10 und mit Rücksicht darauf, daß gleiche Kugeln gegeneinander gedrückt werden, ϑ1 = ϑ2, ferner ρ1 = ρ2, so gehen die Gleichungen 1 und 2 über in die Form:
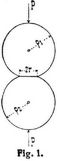
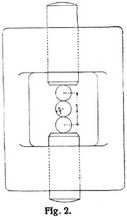
Vielfach werden zwei Kugeln verwendet (Fig. 1), doch ist auch hierbei nicht ausgeschlossen, daß die Bruchfestigkeit noch zu hoch gefunden wird, indem die einseitig in die Druckstempel eingedrückten Kugeln durch das umgebende Material gestützt werden. Am sachgemäßesten ist es daher, die zu prüfende Kugel zwischen zwei andern zu beanspruchen (Fig. 2). Ganz besonders ist beim Versuch zu beachten, daß die Kraftrichtung durch die Mitten der Kugeln gehen muß, um deren Abrollen gegeneinander zu vermeiden. Um dieser Bedingung zu genügen, hat Rudeloff, der zuerst mit drei Kugeln arbeitete, folgende Einrichtungen angegeben, die in der Ausführungsform von Amsler auch Stribeck [5]–[7] und Schwinning [8] zu ihren Versuchen[745] benutzt haben. In einem kräftigen Bügel (Fig. 2) sind zwei Druckstempel konzentrisch zueinander gehalten. Ihre Druckflächen besitzen Körnerlöcher, in die die beiden äußeren der drei Kugeln sich einlegen. Diese Löcher werden, sofern die Druckstempel so geführt sind, daß sie sich nicht gegeneinander verdrehen können, am bellen angebracht, indem man eine Kugel von der Größe der zu prüfenden gleichzeitig in beide Druckflächen eindrückt. Zum Ausrichten der dritten mittleren Kugel dient ein winkelförmiges Lineal und ein Gegenstück mit ebener Fläche; die Länge beider ist etwas geringer als der dreifache Kugeldurchmesser. Handelt es sich darum, beim Versuch mehrfach bis auf Null zu entlasten, so umgießt man die in das Winkellineal hineingelegten und von Hand leicht zusammengedrückten Kugeln vor dem Einbringen zwischen die Stempel mit Gips. Die Gefahr, daß die Kugeln beim Entlasten herausfallen, ist dann ausgeschlossen, selbst wenn der Gips zum Ansetzen von Meßapparaten stellenweise entfernt wird, so daß Teile der Kugeloberflächen frei liegen.
Die erste Veröffentlichung über Untersuchungen von Stahlkugeln stammt von Rasch [1]. Er arbeitete mit je zwei Kugeln und ermittelte die Durchmesser der Druckflächen für verschiedene Belastungen mit Hilfe eines Zeißschen Komparators bis auf etwa 0,001 mm. Aus den Ergebnissen seiner Versuche mit Kugeln verschiedenen Durchmessers und verschiedener Härte weist er nach, daß die obengenannte Voraussetzung 2, unter der die Formeln von Hertz Gültigkeit haben, nur für ganz geringe Belastungen P zutrifft. Die Größe der Druckfläche nimmt daher in Wirklichkeit mit wachsendem P wesentlich schneller zu, als die Rechnung nach der Hertzschen Formel es ergibt. – An Stelle der letzteren stellt Rasch die Formel auf
In ihr sind γ und n Materialkonstanten, zwischen denen bei harten Gußstahlkugeln die Beziehung besteht:
Ferner ergab sich, daß γ vom Kugelhalbmesser nahezu unabhängig ist und daß man bei harten Gußstahlkugeln für praktische Zwecke mit hinreichender Genauigkeit setzen kann: γ = 0,03122 und n = 3/8. Der Halbmesser der Druckfläche ergibt sich dann zu:
Die Zerstörung der Kugeln, durch Eintreten von Rissen, fand nahezu bei ein und derselben Spannung (σmax = P/r2π) statt, gleichgültig welchen Durchmesser die Kugeln hatten. Die geringe Abnahme von σ mit wachsendem ρ schreibt Rasch dem Umstande zu, daß kleinere Kugeln der schnelleren Abkühlung wegen eine gründlichere Härtung erfahren als Kugeln mit größerem Durchmesser. Als mittlere Fertigkeit guter Stahlkugeln fand Rasch: σmax = 815 kg/qmm. Stribeck maß bei seinen Druckversuchen mit je drei Kugeln von gleichem Durchmesser die Längenänderungen auf 4ρ (Meßlänge l, s. Fig. 2, gleich Durchmesser der mittleren Kugel je einem Halbmesser der beiden Endkugeln) mit Martensschen Spiegelapparaten. Unter stufenweiser Laststeigerung wurde bei jeder Laststufe so oft be- und entlastet, bis für die Längenänderungen (= 2 δ/2) gleichbleibende Werte erhalten wurden. Unter der Einführung des Wertes für die Dehnungszahl des Materials 1/21200 in die Rechnung wurden die Werte für δ/2 nach der obigen Formel von Hertz berechnet und mit den Beobachtungen verglichen. Hierbeiergaben sich nach Ueberschreitung der Elastizitätsgrenze die gesamten Zusammendrückungen größer, die elastischen kleiner als die berechneten. Die Unterschiede waren aber selbst nach beträchtlicher Ueberschreitung der Proportionalitätsgrenze nicht groß. Die Belastungen bei Eintritt der Elastizitätsgrenze waren den Quadraten der Durchmesser proportional, die Druckspannungen für alle Kugeldurchmesser also gleich groß.
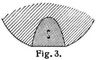
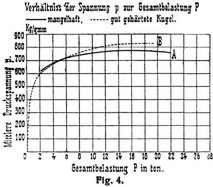
Schwinning fordert, daß die vollständige Kugelprüfung sich erstrecken soll auf 1. die Beurteilung des Bruchausschens, 2. die Bestimmung der »Sprungbelastung«, d.h. der Belastung beim Eintritt des ersten Sprunges, 3. der Bestimmung der Zähigkeit, und 4. auf die Feststellung der mittleren Druckspannung in der Druckfläche bei verschiedenen Belastungen. Nach dem Bruchausschen soll die Güte und Gleichmäßigkeit der Härtung beurteilt werden. In der Regel brechen die Kugeln genau diametral durch, dabei scheren unter den beiden Druckflächen häufig Druckkegel S (s. Druckversuch) aus (Fig. 3). Nach Schwinning entstehen diese Kegel nur dann, wenn die Belastung stetig, d.h. ohne Unterbrechung durch Entlasten, bis zum Bruch der Kugel gesteigert wird. Zugleich ist dann auch die Bruchlast größer, als wenn öfteres Entlasten stattfindet. Erklärt wurden diese Erscheinungen damit, daß der diametrale Sprung bei ununterbrochener Laststeigerung bereits eintritt, bevor die Höchstlast erreicht ist, daß aber die Reibung an den Druckflächen das Zerfallen der gesprungenen Kugel hindert, bis bei weiterer Laststeigerung die Scherkegel entstehen und nun sprengend wirken. Beim Versuch mit häufigem Entlasten dagegen krümmen sich die Druckflächen wieder etwas, so daß die starke Reibung aufgehoben wird und der Zerfall nun ungehindert und zwar beim Entlasten erfolgen kann. Die Bruchlast P wird daher bei öfterem Entlasten um etwa ein Viertel geringer gefunden als bei ununterbrochener Laststeigerung. Weit wichtiger als P hält Schwinning die »Sprungbelastung«,[746] weil die Kugeln im Betrieb durch Ausbrechen zerstört werden. Bei Verwendung von zwei Kugeln ist der erste Sprung stets ein die Druckfläche umgebender Kreisriß. Er tritt häufig schon bei Belastungen ein, die gleich einem Zehntel der Bruchlast sind. Um den Riß besser zu erkennen, empfiehlt sich Anätzen mit verdünnter Salzsäure. Dieselbe Kugel kann für verschiedene Belastungen verwendet werden; die einzelnen Druckstellen werden dann vor dem Anätzen zweckmäßig durch Lackringe gekennzeichnet. Bei Bestimmung der Bruchlast unter Verwendung von drei Kugeln ergab sich in Uebereinstimmug mit der Beobachtung von Rasch [1], daß der Kugeldurchmesser, die Krümmung, ohne wesentlichen Einfluß auf die Bruchspannung p = P/f in der Druckfläche f ist. Die beobachteten Festigkeitsunterschiede führt auch Schwinning auf Unterschiede in der Härtung zurück. Bei Kugeln mit dünner harter Oberfläche und weichem Innern erreicht p mit wachsender Belastung einen Höchstwert, sobald die Druckfläche so groß geworden ist, daß auch der weiche Kern Einfluß gewinnt, dann nimmt p wieder ab (s. Fig. 4, Linie A). Bei gutgehärteten Kugeln dagegen (Linie B, Fig. 4) wird pmax erst annähernd mit dem Bruch erreicht. Daher soll p für mehrere Laststufen ermittelt werden, um den Höchstwert zu finden. Unter Zähigkeit Z versteht Schwinning die Arbeitsaufnahme, bezogen auf die Volumeneinheit bis zum Eintritt des erden Sprunges in der mittleren der drei Kugeln, wobei für Z die Gleichung gilt:
Die Größe der zulässigen Belastung P der Kugeln im Lager ist nur durch Versuche mit Lager zu ermitteln. Sie ergab sich zu P = k D2, also proportional dem Quadrat des Kugeldurchmessers. Hierbei hängt der Koeffizient k von der Form der Laufrinne ab. Betrug deren Krümmungshalbmesser 2/3 D, so ergab sich k = 100, also P = 100 D2; für ebene, kegelförmige oder zylinderförmige Laufringe war dagegen k = 30 – 50.
Literatur: [1] Rasch, Prüfung von Gußstahlkugeln, Zeitschr. für Werkzeugmaschinen und Werkzeuge 1899, Heft 19 u. 20. – [2] Hertz, Ueber die Berührung fester elastischer Körper, Journal für die reine und angewandte Mathematik 1881, Bd. 92, S. 156–171. – [3] Ders., Ueber die Berührung fester elastischer Körper und über die Härte, Verhandlungen des Vereins zur Beförderung des Gewerbefleißes, 1882, S. 449. – [4] Ders., Gesammelte Werke, Bd. 1, S. 155. – [5] Stribeck, Kugellager für beliebige Belastungen, Mitteil. a. d. Zentraldelle für wissenschaftlich-technische Untersuchungen 1900, Heft 1. – [6] Ders., Kugellager für beliebige Belastungen, Zeitschr. d. Ver. deutsch. Ing. 1901, S. 73. – [7] Ders., Ann. für Gewerbe und Bauwesen 1901, Bd. 49, S. 2. – [8] Schwinning, Versuche über die zulässige Belastung von Kugeln und Kugellagern, Zeitschr. d. Ver. deutsch. Ing. 1901, S. 332.
Rudeloff.
http://www.zeno.org/Lueger-1904.