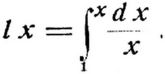Logarithmus

Logarithmus einer Zahl a zur Balis b ist die Zahl x, mit der b potenziert werden muß, um a zu erhalten; aus b^x = a folgt x = log a/_b oder kurz x = log a, wenn sich die Basis b von selbst versteht. Die Zahl a heißt Numerus von x.

Es gelten die Formeln

was auch die Basis sein möge. Hieraus ergibt sich, daß die Logarithmen zur Vereinfachung von Rechenoperationen dienen: die Multiplikation wird mit ihrer Hilfe auf eine Addition zurückgeführt u.s.w. Man benutzt zu diesem Zweck Logarithmen, welche einem Logarithmensystem angehören, d.h. welche alle dieselbe Basis haben.

Am gebräuchlichsten sind die Briggschen Logarithmen mit der Basis 10, welch letztere als selbstverständlich nicht angegeben wird. Die Logarithmen der ganzen positiven und negativen Potenzen von 10 sind positive und negative ganze Zahlen, z.B. log 10 = 1; log 100 = 2; log 0,001 = – 3. Die Logarithmen der übrigen positiven Zahlen sind Brüche, welche positiv/negativ sind, je nachdem der Numerus 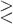1 ist. Dieselben bestehen aus einer ganzen Zahl (Kennziffer) und einem stets positiv genommenen Dezimalbruch (Mantisse). Zahlen, welche sich nur in der Zahl der angehängten Nullen oder in der Stellung des Komma unterscheiden, haben gleiche Mantissen, z.B. log 3 = 0,47712; log 3000 = 3,47712; log 0,0003 = 0,47712 – 4. An Stelle der negativen Kennziffern pflegt man jedoch positive zu setzen und –10 hinzuzufügen; die letztere Zahl wird als selbstverständlich häufig weggelassen; z.B. log 0,0003 = 6,47712–10; log 0,3 = 9,47712–10 oder kurz 9,47712. Bei ganzen Zahlen und unechten Brüchen beträgt alsdann die Kennziffer des Logarithmus eine Einheit weniger, als Stellen vorhanden sind bezw. dem Komma vorangehen; bei echten Brüchen hat man von 9 die Zahl der Nullen abzuziehen, welche dem Komma folgen. Zur Berechnung der Logarithmen wandte man anfangs die mühsame Interpolation, später die leichtere Reihenentwicklung an. Die berechneten Logarithmen hat man in Tafeln (Logarithmentafeln) zusammengestellt. Von denselben sind die gebräuchlichsten die fünfstelligen, welche direkt die Logarithmen aller vierstelligen Zahlen (und aller mit 4 bedeutsamen Ziffern) geben. Die Logarithmen mehrstelliger Zahlen werden mit Hilfe der Proportionaltäfelchen berechnet, deren Einrichtung auf der Formel

beruht; diese gilt näherungsweise, wenn b und c gegen a sehr klein sind.

[196] Beispiel a = 24340; b = 3; c = 10. log (a + c) = log 24350 = 4,38650; log a = 4,38632. Differenz (sogenannte Tafeldifferenz) 18. Nun geben die Proportionaltäfelchen 18 · b/c = 18 · 0,3 = 5,4; also log 24343 = log (a + b) = log a + 5,4 = 4,34637.

Die Tafeln dienen auch zur Aufsuchung des Numerus, wenn der Logarithmus gegeben ist, doch benutzt man hierfür auch Antilogarithmen (s.d.). Zur logarithmischen Rechnung müssen mathematische Ausdrücke möglichst in Produkte, Quotienten, Potenzen, Wurzeln verwandelt werden, wogegen Summen und Differenzen vermieden werden. Man schreibt daher

u.s.w. Weil sich log (a ± b) nicht umformen läßt, vermeidet man bisweilen das fortwährende Zurückgehen auf den Numerus durch Anwendung von Additions- und Subtraktionslogarithmen (s d.).

Die Logarithmentafeln enthalten meistens auch die Logarithmen der trigonometrischen Funktionen, ferner Quadratzahlen, mathematische und physikalische Konstante u.a.

Natürliche (Napiersche, hyperbolische) Logarithmen heißen diejenigen mit der Basis e = c = 2,71828 ... (s. Exponentialfunktion). Sie werden kurz mit l bezeichnet. Es ist daher x = l a, wenn a = e^x. Sie spielen in der Analysis und Funktionentheorie eine große Rolle; für technische Rechnungen werden sie nicht so häufig gebraucht.

Die Logarithmusfunktion wird durch Integration von 1/x erhalten: es ist

Wegen l ∞ = + ∞; l 0 = – ∞ besitzt sie die beiden Unstetigkeitspunkte 0 und ∞, in welchen die ∞ Blätter der Riemannschen Fläche zusammenhängen (s. Funktionen). Es ist

wo n eine beliebige positive oder negative Zahl. Der Logarithmus ist also unendlich vieldeutig. Speziell ist l i = π i/2; l (–1) = π i; l (–i) = 3π i/2 Die Logarithmen der negativen Zahlen sind also imaginär, zum Beispiel l (–e) = 1 + π i u.s.w. Die Formel l x + l y = l (x y) heißt Additionstheorem der Logarithmusfunktion.

Literatur: [1] Claussen, Die Logarithmen und ihre Anwendung, Leipzig 1879. – [2] Kleyer, Lehrbuch der Logarithmen, Stuttgart 1884. – [3] Meyer, M., Katechismus der Logarithmen, 2. Aufl., Leipzig 1898. – [4] Stadthagen, Ueber die Genauigkeit logarithmischer Berechnungen, Berlin 1888. – Logarithmentafeln sind: [5] Vega, Thesaurus logarithmorum, Leipzig 1794. – [6] Ders., Logarithmisch-trigonometrisches Handbuch (siebenstellig), 81. Aufl., Berlin 1906. – [7] Schrön, Siebenstellige gemeine Logarithmen, 25. Aufl., Braunschweig 1904. – [8] Bremiker, Logarithmisch-trigonometrische Tafeln mit sechs Dezimalstellen, 13. Aufl., Berlin 1900. – [9] Gauß, Fünfstellige, vollständige logarithmische u. trigonometrische Tafeln, 94. Aufl., Halle 1906. – [10] Rex, Fünfstellige Logarithmentafeln, Stuttgart 1884. – [11] Wittstein, Fünfstellige logarithmisch-trigonometrische Tafeln, 17. Aufl., Hannover 1896. – [12] Henrici, Vierstellige logarithmisch-trigonometrische Tafeln, Leipzig 1882.

Wölffing.