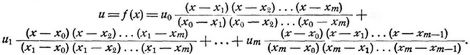- Interpolation
Interpolation, die Berechnung von Zwischenwerten einer Funktion, wenn für eine endliche Anzahl von Werten des Arguments die zugehörigen Funktionswerte gegeben sind.
[206] Bilden die zu den m + 1 gegebenen Funktionswerten u0 u1 ... um gehörigen Argumente x0 x1 ... xm eine arithmetische Reihe, so daß xn = x0 + n d ist, so bildet man von der Reihe u0 u1 ... um die Differenzreihen und bedient sich der Newtonschen Interpolationsformelun = u0 + (n1) Δu0 + (n2) Δ2u0 + ... + Δnu0. Diese Formel liefert genau die gegebenen Funktionswerte für n = 1 ... m; sie liefert genähert die Funktionswerte für andre Werte von u. Für gebrochene und negative n geht sie in eine unendliche Reihe über: un = u0 + (n1)Δu0 + ... in infinitium. Die Binomialkoeffizienten werden in dieser Reihe (zumal für gebrochene n) als Interpolationskoeffizienten bezeichnet. Werte von solchen sind in [3] berechnet. In andrer Bezeichnung macht man nach dem Vorgang von Encke [2] von dieser Reihe in der Astronomie Gebrauch, wobei man den Ausgangspunkt der Differenzen in die Mitte der gegebenen Funktionswerte verlegt. Bilden die Argumente x0 ... xm keine arithmetische Reihe, so bedient man sich zur Interpolation der Lagrangeschen Formel:
Auch diese Reihe liefert die Funktionswerte genau für die Argumente x0 x1 ... xm; für andre Argumente ist der Fehler am kleinsten, je näher der Wert u in der Mitte der gegebenen u0 ... um liegt. Sind ferner x0 ... xm die Wurzeln einer Gleichung (m + 1) Grades F(x) = 0, so kann man auch schreiben:
Soll die Funktion f(x) als periodische Reihe dargestellt werden, so hat man
zu setzen. Die Interpolation dient zur Berechnung von Logarithmen- und andern Tafeln, im kleinen auch bei der Aufsuchung von Zwischenwerten in solchen Tafeln. Ferner findet sie ausgedehnte Anwendung in der Astronomie.
Literatur: [1] Gauß, Werke, Bd. 3, Göttingen 1866. – [2] Brünnow, Lehrb. der sphärischen Astronomie, 4. Aufl., Berlin 1880. – [3] Peters, C.F.W., Astronomische Tafeln und Formeln, Hamburg 1871. – [4] Markoff, A., Differenzenrechnung, deutsch von Friesendorff und Prümm, 1. Teil, Leipzig 1896. – [5] Diestel, F., Beiträge zur Interpolationsrechnung, Göttingen 1890. – [6] Mauderli, S., Die Interpolation und ihre Verwendung bei der Benutzung und Herstellung mathematischer Tabellen, Solothurn 1906.
Wölffing.
http://www.zeno.org/Lueger-1904.