Plattenbalken

Plattenbalken. Als solche werden im Eisenbetonbau die mit einer darüber liegenden Deckenplatte starr verbundenen und statisch zusammenwirkenden Balkenrippen bezeichnet.

Die Bewehrung der Plattenbalken ist sowohl den Biegungsmomenten als auch den Querkräften anzupassen. Ueber die Berechnung der Beanspruchungen infolge der Momente, s. Betoneisenkonstruktionen, Bd. 1, S. 739 ff. Zur Aufnahme der Querkräfte dienen die Bügel (s.d., S. 111) und die abgebogenen Eisen.

Wird ein durch gerade Eisen armierter Plattenbalken der Biegung unterworfen, so bilden sich bei genügend starker Armierung außer[611] den annähernd vertikalen Biegungsrissen in der Mitte auch noch schräge Risse in der Nähe der Auflager (Fig. 1). Die letzteren Risse, die man auch als Schubrisse bezeichnet, sind etwa unter 45° nach oben gerichtet; sie steigen viel rascher in die Höhe und treten dann auf, wenn die Schubspannung etwa gleich der Zugfestigkeit des Betons geworden ist. Die Schubriffe, die vor den Biegungsrissen zum Bruch führen können, treten also infolge der schiefen Hauptzugsspannungen auf, die nach der üblichen Theorie gleich den Schubspannungen gesetzt werden. Denkt man sich die normalen Zugspannungen des Betons von den unteren Eisen aufgenommen, so ergibt sich nach der Formel für die Hauptzugspannungen

σ_I = σ/2 ± √(σ²/4 + τ²),

da σ = 0 vorausgesetzt wird

σ_I = σ_II = τ

und die Richtung der Hauptspannungen unter 45°. Die Hauptzugspannung wird nun zweckmäßig durch die unter 45° abgebogenen Eisen aufgenommen, welche die schrägen Schubriffe annähernd senkrecht kreuzen. Die Momente werden gegen das Auflager kleiner, so daß die unteren Eisen durch solche Aufbiegungen daselbst vermindert werden können.

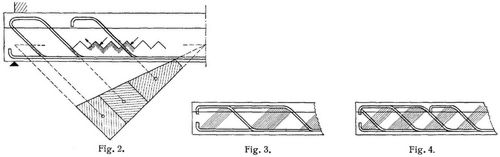
Nach Fig. 2 sind alle auf die nach der Mitte unter 45° anzeigenden Flächenelemente wirkenden Zugkräfte zu addieren und den abgebogenen Eisen zuzuweisen. Auf die andern nach der Mitte fallenden Flächenelemente des Verzahnungsschnittes wirken Druckspannungen, die vom Beton selbst übertragen werden können. Die schiefen Zugkräfte, die nach der Mitte hin bei gleichmäßiger Belastung stetig bis Null abnehmen, können durch den Inhalt der schraffierten Trapezfläche dargestellt werden. Die Abbiegungen sind dann so zu legen, daß sie durch die Schwerpunkte der Einzeltrapeze hindurchgehen.

Der Eisenbetonbalken kann in dieser Anordnung auch als Fachwerkbalken mit einfachem oder doppeltem Strebensystem (Fig. 3 und 4) betrachtet werden, wobei die schraffierten Betonstreifen die Druckstreben vorstellen. Man erhält die gleiche Zugkraft in den abgebogenen Eisen, ob man die Querkraft in die Richtung der Diagonalen zerlegt, ähnlich wie beim Parallelträger einfachen oder mehrfachen Systems, oder ob man sie aus der Schubspannung τ₀ (nach Fig. 2) rechnet.

Da die Abbiegungen tatsächlich auf Zug beansprucht sind, so ist die Adhäsions- oder Haftspannung an den unteren Eisen in andrer Weise zu berechnen, als wenn alle Eisen gerade durchgingen. Statt der Formel für die Haftspannung

gilt, wenn die schiefen Zugspannungen ganz durch abgebogene Eisen nach dem einfachen doppelten oder mehrfachen Strebensystem aufgenommen werden, die Formel

wo u den Umfang der unteren geraden Eisen bedeutet. Die Versuche haben die Richtigkeit dieser Formel bestätigt.

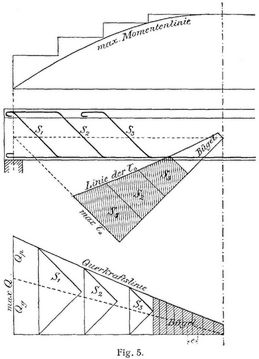
Da man einem Plattenbalken in allen Teilen mindestens die gleiche Bruchsicherheit wie in der Mitte geben soll, so kann man auf die schiefe Zugfestigkeit des Betons in der Nähe der Auflager nicht rechnen, wenn sie vor Erreichung des Bruchs in der Mitte überschritten würde. Ueberschreitet also die Schubspannung τ₀ den vierten Teil der Zugfestigkeit, also etwa 3–4 kg/qcm, so sind alle schiefen Zugkräfte durch abgebogene Eisen, eventuell in Verbindung mit Bügeln, aufzunehmen. Man hat demnach beim Entwerfen eines einfachen, frei aufliegenden Plattenbalkens nach Fig. 5 und Fig. 6 zu verfahren. In Fig. 5 ist ein doppeltes Strebensystem vorausgesetzt, bei dem die abgebogenen Strecken S₁, S₂ und S₃ die schiefen Zugspannungen ganz aufnehmen sollen. Die Kräfte S₁, S₂ und S₃ sind dann durch die mit der Stegbreite b₀ zu multiplizierenden Inhalte der schraffierten τ₀ Flächen dargestellt. An Hand der Maximalmomentenlinien hat man[612] gleichzeitig zu prüfen, ob überall noch eine hinreichende Tragfähigkeit hinsichtlich der Biegungsmomente vorhanden ist. Dies geschieht am einfachsten, indem man bei der Momentenfläche zum Vergleich die Fläche derjenigen Momente aufzeichnet, die der Balken an den verschiedenen Stellen aufnehmen könnte, sofern die untere Eisenmenge bis zur zulässigen Grenze beansprucht wäre. Der Sicherheit wegen nimmt man dabei die abgebogenen Eisen schon an der unteren Ecke als für das Moment nicht mehr wirksam an. Wenn man die Abbiegungen so anordnet, daß sie die gezogenen Diagonalen eines doppelten Strebenfachwerkes bilden, so können die Kräfte S₁, S₂ und S₃ auch durch Zerlegung der Querkräfte der betreffenden Felder nach den zwei unter 45° verlaufenden Richtungen gefunden werden, wie dies in Fig. 5 unten dargestellt ist.

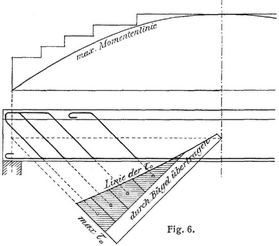
Da man meist mit partieller Nutzlast zu rechnen hat, so ist τ₀ in der Mitte nicht = o und man muß dann in der Nähe der Mitte zur Aufnahme der Querkräfte Bügel (s.d.) heranziehen, die außer den abgebogenen Eisen immer angewendet werden. In Fig. 6 ist vorausgesetzt, daß die abgebogenen Eisen gleichen Querschnitt besitzen, so daß sie gegen das Auflager hin näher beieinander liegen.

Literatur: [1] Mörsch, Zeitschr. Beton und Eisen 1903, Heft 4. – [2] Ders., Deutsche Bauzeitung 1907 Nr. 30, 32 und 35. – [3] C. v. Bach, Versuche mit Eisenbetonbalken, Berlin 1907, Mitteilungen über Forschungsarbeiten, Heft 39, 45–47. – [4] C. v. Bach und O. Graf, Versuche mit Eisenbetonbalken zur Ermittlung der Widerstandsfähigkeit verschiedener Bewehrung gegen Schubkräfte, Heft 10 und 12, Berlin 1911, Heft 20, Berlin 1912. – [5] Mörsch, Eisenbetonbau, 4. Aufl., Stuttgart 1912. – Saliger, Schubwiderstand und Verbund von Eisenbetonbalken auf Grund von Versuchen und Erfahrungen, Berlin 1913.

Mörsch.

Fig. 1.

Fig. 2., Fig. 3., Fig. 4.

Fig. 5.

Fig. 6.