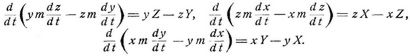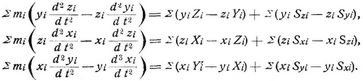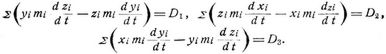Prinzip der Flächen

Prinzip der Flächen. Das Prinzip bezieht sich auf ein freies System, das nur inneren Bedingungen unterworfen ist. In seiner Formulierung bedarf man der Begriffe Kraftmoment (Bd. 5, S. 653) und Moment der Bewegungsgröße (s. Moment, Bd. 6, S. 475). Es lautet dann: In bezug auf eine beliebige feste oder auch auf eine sich selbst parallel bleibende, stets durch den Schwerpunkt des Systems gehende Achse ist in jedem Augenblick die zeitliche Aenderung des Momentes der Bewegungsgröße sämtlicher Massen gleich dem Moment der äußeren Kräfte. Ist insbesondere das Moment der äußeren Kräfte in bezug auf eine solche Achse dauernd gleich Null, so ist das Moment der Bewegungsgröße in bezug auf diese Achse konstant. Das Prinzip gilt übrigens ebenso, wenn man statt der Momente um eine Achse die gerichteten Momente in bezug auf einen festen Punkt oder auf den mit dem System sich bewegenden Schwerpunkt nimmt.

[238] Am einfachsten wird das Prinzip für einen einzelnen freien Punkt. Kombiniert man seine drei Bewegungsgleichungen

in der Weise paarweise miteinander, so daß man erhält

so sind die linken Seiten dieser Gleichungen totale Differentialquotienten, und es wird

Sind nun die Kräfte X, Y, Z so beschaffen, daß eine, zwei oder drei Kraftmomente in bezug auf die Koordinatenachsen verschwinden y Z – z Y = 0, z X – x Z = 0, x Y – y X = 0, so erhält man ebensoviel Integrale der Bewegungsgleichungen, nämlich

Dieser Satz heißt, mit Rücksicht auf seinen geometrischen Sinn, das Prinzip der Flächen. Man erhält daher ein oder drei Integrale der Bewegungsgleichungen, je nachdem eine oder zwei solcher Kraftmomente verschwinden. Sind alle drei gleich Null, so liefert die Multiplikation derselben mit x, y, z und ihre Addition D₁ x + D₂ y + D₃ z = 0, d.h. der Punkt bewegt sich in einer durch den Koordinatenursprung gehenden Ebene und seine Bewegung ist eine Zentralbewegung. Die Integrale haben folgende Bedeutung, z.B. die dritte: x d y – y d x = D₃ d t. Der Ausdruck links bedeutet, wie man beim Uebergang zu Polarkoordinaten alsbald steht, den doppelten unendlich kleinen Sektor, welchen der Radiusvektor, der den Ursprung mit dem Punkte x y verbindet, im Zeitelement d t beschreibt. Dieser Sektor ist daher ¹/₂ D₃ d t, d.h. dem Zeitelemente proportional, in welchem er beschrieben wird. Es ist also sein Integral ¹/₂ D₃ (t – t₀) der in der Zeit t – t₀ beschriebene endliche Sektor, und ähnliches gilt für die andern Koordinatenebenen. Weil die Bedeutung der so zu erhaltenden weiteren Integrale Flächenräume (der Zeit proportionale Sektoren) darstellt, führt das Prinzip den Namen des Prinzips der Flächen. Kombiniert man in ähnlicher Weise die Bewegungsgleichungen eines Massenpunktsystems und summiert sie durch das ganze System hindurch, so erhält man

Die linken Seiten dieser Gleichungen sind auch hier Differentialquotienten der Komponenten des Momentes der. Bewegungsgrößen nach der Zeit, nämlich

Die rechten Seiten sind die Komponenten des Momentes der äußeren und Verbindungskräfte. Bei einem freien System verschwindet aber das Moment der Verbindungskräfte (und auch der inneren Kräfte), da diese nach dem d'Alembertschen Prinzip stets ein Gleichgewichtssystem bilden. Reduzieren sich auch die Komponenten der äußeren Kräfte sämtlich oder teilweise auf Null, so erhält man ein oder drei Integrale der Bewegungsgleichungen, nämlich

Anwendungen: 1. Ein starrer Körper bewegt sich unter dem Einfluß der Schwere so, daß das gerichtete Moment der Bewegungsgröße in bezug auf den Schwerpunkt, der sogenannte Drehimpuls, dauernd konstant bleibt, weil die Schwerkräfte in bezug auf den Schwerpunkt das Moment Null besitzen. Hat der Körper von Anfang keine Drehung, so erhält er auch durch die Schwerkräfte keine.

2. Ein durch innere Kräfte beweglicher Körper, z.B. ein lebendes Wesen, kann sich unter gleichen Verhältnissen eine beliebige Drehung verschaffen, wenn es imstande ist, relative Drehbewegungen einzelner Teile so vorzunehmen, daß nach Ablauf einer ganzen oder mehrerer Umdrehungen derselben wieder die ursprüngliche Konfiguration des Körpers hergestellt wird. Eine mit dem Rücken nach unten fallende Katze kann z.B. durch rasche Drehung des senkrecht zur Körperachse gehaltenen Schwanzes um diese Achse den Körper in entgegengesetzter Richtung drehen und dadurch die Füße nach unten kehren.

3. Ein Akrobat, der beim Absprung mit gestrecktem Körper eine schwache Drehbewegung um eine horizontale Achse durch den Schwerpunkt erhält, kann diese durch Anziehen der Arme und Beine unter Erhaltung des Momentes der Bewegungsgröße um die genannte Achse erheblich verstärken und damit einen Salto mortale schlagen.

4. Ein mit einer Kolbenmaschine ausgerüstetes Schiff, das sich in Ruhe bezw. gleichförmiger Bewegung befindet, wird beim Ingangsetzen der Maschine Schwankungen ausführen, die mit jenen der Kolben das Moment Null der Bewegungsgröße in bezug auf einen beliebigen Punkt des Schiffes ergeben. Damit diese lästigen Schwankungen nicht auftreten, müssen die [239] Bewegungen der Kolben so erfolgen, daß ihr gemeinsamer Schwerpunkt in Ruhe bleibt und das Moment der Bewegungsgröße der bewegten Kolben jederzeit verschwindet. Bei vier Kolben ist das durch geeignete Wahl der Abstände der Kolbenachsen und der Kurbelstellungen stets zu erreichen (Schlickscher Massenausgleich bei Schiffsmaschinen).

Literatur: Schell, Theorie der Bewegung und der Kräfte, 2. Aufl., Leipzig 1879, Bd. 1, S. 352–355, Bd. 2, S. 521–526; Budde, Allgem. Mechanik, Berlin 1890, Bd. 1, S. 348–354; Appell, Traité de mécanique rationnelle, Paris 1896, Bd. 2, S. 76–79; Föppl, Vorlesungen über techn. Mechanik, Bd. 4, Dynamik, Leipzig 1901, S. 117–179.

Finsterwalder.