Verschiebungspläne

Verschiebungspläne (nach dem Verfahren von Williot) dienen zur Ermittlung der elastischen Verschiebungen der Knotenpunkte ebener Fachwerke.

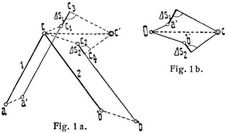
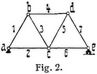
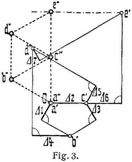
Die Verschiebungen der Knotenpunkte eines Fachwerks entstehen aus den elastischen Verlängerungen ∆ s der einzelnen Stäbe. In Fig. 1a ist der Knotenpunkt c mit den Knotenpunkten a und b durch die beiden Stäbe 1 und 2 verbunden, deren Längen s₁ und s₂ sich um ∆ s₁ und – ∆ s₂ ändern, während die beiden Punkte a und b in die neuen Lagen a' und b' rücken. Die neue Lage c' des Punktes c findet sich dann wie folgt. Zunächst verschiebt man die beiden Stäbe 1 und 2 parallel zu sich selbst in die Lagen a' c₁ und b' c₂, hierauf ändert man die Längen in der vorgeschriebenen Weise, d.h. wenn Stab 1 um ∆ s₁ länger wird, so fügt man c₁ c₃ = ∆ s₁ an, während man, wenn Stab 2 um ∆ s₂ kürzer wird, die Strecke c₂ c₄ = ∆ s₂ in Abzug bringt. Mit den neuen Stablängen a' c₃ und b' c₄ beschreibt man nun um a' und b' Kreisbögen. Der Schnittpunkt c' jener Bögen ist die neue Lage des Punktes c. In dem hier vorausgesetzten Falle verschwindend kleiner elastischer Verschiebungen dürfen die Kreisbögen durch die auf den Geraden a' c₃ und b' c₄ errichteten Lote ersetzt werden. Es empfiehlt sich nun, die gesuchte Verschiebung c c' in einer besonderen Figur (1b) mit genügender Vergrößerung darzustellen. Von einem beliebigen Punkt O aus (Ursprung oder Pol) trägt man die gegebenen Verschiebungen O a' = aa' und O b' = bb' der Punkte a und b nach Größe, Richtung und Sinn auf. An die Polstrahlen O a' und O b' füge man in a' und b' die den Stäben 1 und 2 parallelen Längenänderungen ∆ s₁ und ∆ s₂ an und errichte in deren Endpunkten Lote, die sich in c' schneiden. Alsdann ist die Verschiebung des Knotenpunkts c nach Größe, Richtung und Sinn durch den Polstrahl O c' dargestellt. Die Längenänderungen werden in dem Sinn angetragen, in welchem sie vor sich gehen, c₁ c₃ ist als Verlängerung, c₂ c₄ als Verkürzung des betreffenden Stabes gedacht. Durch wiederholte Lösung dieser Aufgabe ist man imstande, die Verschiebungen aller Knotenpunkte eines Fachwerks zu ermitteln, wenn man einen Knotenpunkt als unverändert und eine Stabrichtung als gleichbleibend annimmt In dem kleinen Fachwerke Fig. 2 werde zunächst Stab 2 als horizontal bleibend und Punkt a als unverschieblich angenommen. Von dem Punkt O bezw. a' ausgehend (Fig. 3) wird zunächst die Verlängerung ∆ 2 des Stabes 2 aufgetragen, dann ist O c' die Verschiebung des Punktes c. Nach dem Vorhergehenden erhält man die Verschiebung des Punktes b, der mit a und c durch die Stäbe 1 und 3 verbunden ist, indem man von O aus zunächst die Verschiebungen von a und c aufträgt, was schon geschehen ist und die Punkte a' und c' lieferte, darauf werden in a' und c' die Längenänderungen ∆ 1 und ∆ 3 angetragen und in ihren Endpunkten Lote errichtet, deren Schnittpunkt b' ist. O b' ist dann die gesuchte Verschiebung des Punktest. Zur Ermittlung der Verschiebung des Punktes d hat man zunächst die Verschiebungen der vorhergehenden Punkte b und c vom Ursprung O aus aufzutragen. Dies ist aber schon durch die Konstruktion der Punkte c' und b' geschehen. Man kann also gleich die Längenänderungen ∆ 4 und ∆ 5 der Stäbe 4 und 5 in b' und c' antragen und die Lote errichten, die als Schnitt den Punkt d' liefern, die Verschiebung des Knotens d ist alsdann durch die Strecke O d' nach Größe, Richtung und Sinn dargestellt. Durch Wiederholung des Verfahrens erhält man auch den Punkt e'.

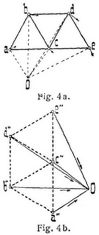
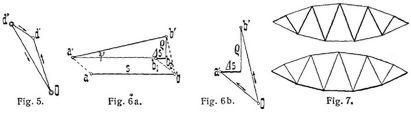
Die Fig. 3, deren Polstrahlen O b' O c' ... nach Größe, Richtung und Sinn die Verschiebungen der Knotende ... darstellen, heißt man den Verschiebungsplan des Fachwerkes (Fig. 2). – Für praktische Zwecke ist die angegebene Lösung noch nicht vollständig. Das Fachwerk Fig. 2 wird nach der Deformation noch auf beiden Auflagern aufsitzen, während nach dem Kräfteplan infolge des als horizontal bleibend angenommenen Stabes 2 sich eine Hebung des Auflagerknotens e ergibt. Um nun die den Auflagerbedingungen entsprechenden Verschiebungen der Knoten zu erhalten, muß das deformierte Fachwerk um den Punkt a so weit nach rechts gedreht werden, bis Punkt e auf seinem Auflager aufsitzt. Würden infolge gewisser andrer Annahmen beim Aufzeichnen des Verschiebungsplanes beide Auflagerpunkte sich abgehoben haben, so würde der entsprechende Drehpunkt für das deformierte Fachwerk ein bestimmter Punkt außerhalb des letzteren sein. – Bei der Drehung um irgendeinen Punkt[781] beschreibt jeder Knoten (Fig. 4a) ein kleines Kreisbogenstück, das mit dem Lot auf der Verbindungslinie zum Drehpunkt verwechselt werden darf. Die Länge des Bogenstückchens ist proportional dem Abstand vom Drehpunkt. Trägt man daher auch die Verschiebungen, die bei der Drehung entstehen, als Strahlen nach einem Pol O hinlaufend auf, so liegen die Punkte a'' b'' c'' d'' e'' auf einer dem Fachwerk ähnlichen, um 90° gedrehten Figur (Fig. 4b). Macht ein Punkt d zwei Verschiebungen, so bestimmt sich die resultierende Bewegung, wenn man die Verschiebungen d'' O und O d' von einem Punkt O aus so aufträgt (Fig. 5), daß die Pfeilrichtungen aufeinander folgen, durch die Strecke d'' d' nach Größe, Richtung und Sinn. Im Williotschen Verschiebungsplan sind die einen Verschiebungen aller Punkte bereits vom Punkt O ausgehend aufgetragen; fügt man daher noch die andern Verschiebungen, die von der nachträglichen Drehung des Fachwerks herrühren, als gegen O hin gerichtete Strahlen hinzu, dann liegen die Endpunkte a'' b'' c'' d'' e'' der letzteren auf einem um 90° gedrehten Fachwerksbild, und die endgültigen Verschiebungen sind durch die Strecken a'' a', b'' b', c'' c' u.s.w. nach Größe, Richtung und Sinn dargestellt. Im vorliegenden Fall ergibt sich Punkt a'' des Trägerbildes aus der Bedingung, daß Knoten a am seiten Auflager überhaupt keine Verschiebung erfahren darf, während e'' nur auf einer Horizontalen durch e' liegen kann, indem die endgültige Verschiebung des Knotens e am beweglichen Auflager nur horizontal sein darf. Aus der Lage von a'' und e'' ergeben sich dann die übrigen Punkte des um 90° gedrehten Trägerbildes. Die Williotschen Verschiebungspläne werden benutzt zur Ermittlung der Einsenkungen von Fachwerken und der dazu gehörigen Einflußlinien (Maxwellscher Satz). Sie spielen eine wichtige Rolle bei der Berechnung statisch unbestimmter Fachwerke.

Eine Abart ist das Stabzugverfahren, wobei die Verschiebungen mit Benutzung der gerechneten Drehungswinkel der einzelnen Stäbe aufgetragen werden. In Fig. 6a sei a b die ursprüngliche Lage eines Fachwerkstabes, dessen Anfangspunkt a sich nach a' verschiebt. Aendert sich gleichzeitig seine Länge um ∆ s und dreht er sich noch um den sehr kleinen Winkel ψ, so findet man die neue Lage des Punktes b, wenn man zunächst den Stab a b in die parallele Lage a' b₁ bringt, dann die Längenänderung b₁ b₂ = ∆ s anfügt und in b₂ ein Lot ρ = b' b₂ = s ψ errichtet. In entsprechend vergrößertem Maßstab in Fig. 6b dargestellt, ersteht man, daß die Verschiebung Ob' des Punktes erhalten wird, wenn man von O aus zunächst die Verschiebung des Anfangspunktes a des Stabes gleich O a' aufträgt, alsdann ∆ s und ρ nach Größe, Richtung und Sinn anfügt. Bei Wiederholung des Verfahrens für die folgenden Stäbe eines Stabzuges hat man dann jeweils nur noch ∆ s und ρ anzutragen, weil die Verschiebungen der Anfangspunkte als Strahlen von O aus schon ermittelt sind. Wie beim Williotschen Plan sind die Verschiebungen der Knotenpunkte wieder durch die von O aus nach den Punkten a' b' c' gehenden Strahlen dargestellt. Die Verschiebungspläne nach dem Stabzugverfahren sind übersichtlicher als nach Williot, dagegen ist die Berechnung der Winkeländerungen ψ zeitraubend. Das Verfahren wird aber genauer, da sich Fehler weniger stark fortpflanzen. Je nachdem die Verschiebungen aller Knotenpunkte oder nur die einer Gurtung des Fachwerkes gesucht werden, wird der Stabzug entsprechend ausgewählt (Fig. 7).

Das Stabzugverfahren kann auch zur Berechnung der Formänderungen biegungsfester, vollwandiger Träger und Bogen Anwendung finden. Man teilt zu diesem Zweck den vollwandigen Träger in eine Anzahl genügend kleiner Teile ein und bestimmt deren Drehungswinkel und Längenänderungen in der Achse, dann kann man den Verschiebungsplan in gleicher Weise aufzeichnen, wie für den Stabzug eines Fachwerks. Die Berechnung der Einflußlinie der Einsenkungen, der statisch unbestimmten Größen von Gewölben u.s.w. kann hiernach leicht graphisch erfolgen.

Literatur: Williot, Notations pratiques sur la statique graphique, Publications scientifiques industrielles, 1877; Mohr, Zivilingenieur 1887; Müller-Breslau, Zeitschr. d. Arch.- u. Ing.-Ver. zu Hannover 1888, S. 605, Stabzugverfahren; Land, Zeitschr. d. Oesterr. Ing.- u. Arch.-Ver. 1888, S. 11 und 162; Müller-Breslau, Graphische Statik der Baukonstruktionen, Bd. 2, 1. Abt., Stuttgart 1905 und Bd. 2, 2. Abt., Leipzig 1908.

Mörsch.

Fig. 1a., Fig. 1b.

Fig. 2.

Fig. 3.

Fig. 4a., Fig. 4b.

Fig. 5., Fig. 6a., Fig. 6b., Fig. 7.