Brachistochrone

Brachistochrone. Zwischen zwei Punkten A und B verschiedener Höhe über der Horizontalebene lassen sich unendlich viele Kurven ziehen, die ein schwerer Punkt durchlaufen kann. Die Brachistochrone ist diejenige von allen, auf welcher der schwere Punkt in der kürzesten Zeit vom höheren Punkte zum niedereren fallend gelangt.

Das Problem der Brachistochrone wird im allgemeinen als ein solches der Variationsrechnung behandelt. Indessen genügen die folgenden elementaren Betrachtungen, um zu zeigen, daß die Brachistochrone zwischen zwei Punkten A und B eine Zykloide ist, deren Ebene in die Vertikalebene dieser Punkte fällt, deren Basis horizontal liegt und welche die Konvexität nach[246] unten kehrt. Nach dem Prinzip der lebendigen Kraft ist die Geschwindigkeit v, welche der Punkt, der von A mit der Geschwindigkeit υ₀ ausgeht, in irgend einem Punkt seiner Bahn annimmt, bloß von der Anfangsgeschwindigkeit υ₀ und der Fallhöhe y abhängig:

1/2 (υ₂ – υ₀²) = gy.

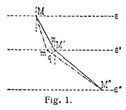
Für alle möglichen, durch A und B gehenden Bahnen wird daher bei gleicher Anfangsgeschwindigkeit die Geschwindigkeit in gleichen Fallhöhen gleich groß sein. Die Kurve kürzesten Falles muß daher notwendig in einer Vertikalebene durch AB liegen, da die andern Kurven zwischen A und B stets größere Bogenelemente haben als ihre Projektion auf die Vertikalebene durch AB und daher zu ihnen als Bahnkurven notwendig größere Fallzeiten gehören. Weiter kann man beweisen, daß, wenn i die Neigung der Tangente eines Punktes M der Brachistochrone gegen die Vertikale und υ dessen Geschwindigkeit ist, die Größe sin i/υ konstant bleibt längs der Brachistochrone (Fig. 1). Denn bedeutet jetzt m einen Punkt in unendlicher Nähe zu M' auf der Ebene ε' in der Schnittlinie der Horizontal-Vertikalebene durch AB mit ε', so ziehe man Mm und mM'' und projiziere m nach p auf MM' und M' nach q auf mM''. Dann wird Mm = Mp und qM'' = M'M'', und es sind die Zeiten, die der bewegliche Punkt braucht, MM' + M'M'' und M m + mM'' + mM'' zu durchlaufen: M M'/v + qM''/υ und Mp/υ + mM''/υ', und ihre Differenz ist pM'/υ – mq/υ' = mM'(sin i/υ – sin i'/υ'), wenn i' die analoge Bedeutung für M' hat, wie i für M. Diese unendlich kleine Zeit ist aber die Aenderung der Fallzeit des beweglichen Punktes beim Uebergang von der Brachistochrone zu einer Nachbarkurve MmM''. Dieselbe muß Null sein, weil die Fallzeit für die Brachistochrone ein Minimum sein muß. Daher folgt sin i/υ = sin i'/υ',–, d.h. sin i/υ ist eine Konstante.

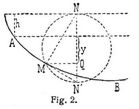
Diese Sätze genügen, um die Zykloide als Brachistochrone zu erweisen. Setzt man sin i/υ = 1/μ, wo also μ konstant ist, und bezeichnet mit υ₀ die Geschwindigkeit auf der Brachistochrone in einem Punkte A (Fig. 2), mit v aber die Geschwindigkeit in einem andern Punkte M, tiefer als A, so hat man nach dem Prinzip der lebendigen Kraft 1/2υ² – 1/2υ⁰₂, wo y die Tiefe von M unter A ist. Setzt man daher in dieser Gleichung

v = μ sin i und

so geht sie über in:

d.h. mit Rücksicht auf die leicht verständliche Figur:

wo N der Schnittpunkt der Normalen der Brachistochrone mit der Niveauebene Null, MN' aber deren Tangente ist. Die Vergleichung dieses Ausdrucks mit sini/υ = 1/μ gibt

oder da 1/2 υ² = g (y + h) ist, 2g · NN' = μ² = 4 g a, d.h. NN' = 2a. Es ist demnach NN' konstant. Ein Kreis also, der die Linie des Niveaus Null berührt und durch M geht, hat einen konstanten Durchmesser 2 a. Hiermit ist aber die Zykloide als Brachistochrone hinreichend charakterisiert, da die vorliegende Konstruktion nichts andres als die Konstruktion der Tangente und Normalen der Zykloide ist.

(Schell) Finsterwalder.

Fig. 1.

Fig. 2.