- Deviationsmomente
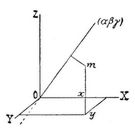
Deviationsmomente. Das Trägheitsmoment J (s.d.) eines Massenpunktsystems ist für alle Achsen des Massenmittelpunktes S bekannt, sobald seine Werte A, B, C für irgend drei zueinander senkrechte Achsen desselben bekannt sind, nebst drei andern Größen D, E, F, die man die Deviationsmomente des Systems für die Achsen nennt. Nimmt man drei solche Achsen als Koordinatenachsen der x, y, z (s. die Figur) an und bildet mit ihnen irgendeine[726] durch S gehende Achse die Winkel α, ß, y, so ist das Trägheitsmoment J des Systems für diese Achse darstellbar unter der Form:
J = A cos 2α + B cos 2ß + C cos 2γ – 2 D cos ß cos γ – 2 E cos γ cos α – 2 F cos α cos ß.
Darin haben die Koeffizienten die Bedeutung:
A = Σ m (y2 + z2),
B = Σ m (z2 + x2),
C = Σ m (x2 + y2),
D = Σ m y z,
E = Σ m z x,
F = Σ m x y.
Ein Deviationsmoment, z.B. F = Σ m x y ist die Summe aller Produkte aus der Masse m eines Punktes des Systems und dem Rechteck, gebildet aus zweien seiner Koordinaten x, y. Je nach der Wahl der Koordinatenachsen sind diese Deviationsmomente positiv oder negativ, können aber auch für drei gewisse Achsen, die Hauptträgheitsachsen, Null werden. Wählt man die Hauptachsen zu Koordinatenachsen, so wird mithin das Trägheitsmoment J durch die einfachere Form dargestellt:
J = A cos 2α + B cos 2ß + C cos 2γ,
worin also A, B, C die Trägheitsmomente für die Hauptachsen oder die Hauptträgheitsmomente bedeuten.
Den Namen Deviationsmomente hat Rankine (A manual of applied mechanics, 4. Aufl., London 1878) gewählt. Eine ausführliche Theorie über die Deviationsmomente lieferte Hâton de la Goupillière (Memoire sur une nouvelle theorie de la geometrie des masses, et sur celle des axes principaux d'inertie), Journal de l'ecole politechnique, XXI, 37. cah., p. 35–96, Paris 1858.
(Schell) Finsterwalder.
http://www.zeno.org/Lueger-1904.