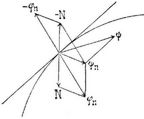
- Druckbeschleunigung
Druckbeschleunigung. Wenn ein Punkt nicht frei der auf ihn wirkenden Beschleunigung ψ folgen kann, sondern durch irgend welche Bedingung genötigt[116] ist, in vorgeschriebener Bahn (Raumkurve) zu laufen, so kann der Zwang, der ihn dazu nötigt, durch eine gewisse Beschleunigung TV ausgedrückt werden. Sie heißt die Widerstandsbeschleunigung oder, wenn der Zwang durch eine Fadenkonstruktion ausgeübt wird, die Spannungsbeschleunigung. Sie liegt, falls keine Reibung wirkt, in der Normalebene zur Bahn und bildet mit der Normalkomponente ψn der gegebenen Beschleunigung ψ als Resultante die in der Schmiegungsebene liegende Normalbeschleunigung φn = v2 : ρ, wenn v die Geschwindigkeit des Punktes und ρ der Krümmungshalbmesser der Bahn ist. Die umgekehrte Widerstandsbeschleunigung – N ist die Druckbeschleunigung des Punktes auf die Bahn. Sie ist (s. die Figur) die Resultante aus der umgekehrten Normal- oder Zentrifugalbeschleunigung – φn und der Normalkomponente ψn der gegebenen Beschleunigung. Im Falle, daß ψ = o, also auch ψn = o, fällt die Druckbeschleunigung mit der Zentrifugalbeschleunigung zusammen. – Es kann vorkommen, daß der Punkt an einer gewissen Stelle die vorgeschriebene Bahn verläßt und die Bewegung desselben in die freie Bewegung übergeht. Damit dies eintrete, ist erforderlich, daß die Druckbeschleunigung Null werde und – φn + ψn = o, d.h. ψn = v2 : ρ werde. An solchen Stellen muß die Beschleunigung ψ in die Schmiegungsebene der Bahn fallen.
Literatur: [1] Schell, Theorie d. Beweg, u. d. Kräfte, Bd. 1, Einleitung.
(Schell) Finsterwalder.
http://www.zeno.org/Lueger-1904.