Druckstäbe

Druckstäbe nennt man die auf Druck beanspruchten Stäbe einer Fachwerkskonstruktion. Bei ihrer Querschnittsbemessung sind die Regeln der Knickfestigkeit (s.d.) zu berücksichtigen.

[138] Ist P die vom Stabe aufzunehmende Druckkraft, F seine Querschnittsfläche, s_k die zulässige Inanspruchnahme mit Rücksicht auf Knickung, die stets kleiner als die zulässige Druckinanspruchnahme s ist, so hat man P = F · s_k. Zur Festsetzung von s_k stehen hauptsächlich zwei Formeln in Anwendung:

1. Die empirische Naviersche (auch nach Schwarz oder Rankine benannte) Formel: s_k = s: (1 + α Fl²/J), worin J das kleinste Trägheitsmoment des Stabquerschnitts, l die freie Knicklänge des Stabes bezeichnet und für Schmiedeeisen gewöhnlich α = 0,0001 gesetzt wird. Für genietete Fachwerksträger kann wegen der teilweisen Einspannung der Stabenden bei der zwischen den Knotenpunkten gemessenen Länge l₁ des Stabes die freie Knicklänge für das Ausknicken in der Tragwandebene l = 0,7 l₁ angenommen werden, wogegen es sich hinsichtlich des Ausknickens senkrecht zur Trägerebene empfiehlt, die ganze Stablänge als Knicklänge einzuführen.

2. Die sogenannte theoretische oder Eulersche Knickfestigkeitsformel, nach der s_k = π² E/β · J/Fl² · s zu wählen ist, wenn unter E der Elastizitätskoeffizient und unter β die Druckfestigkeit des Materials verstanden wird. Hinsichtlich der Knicklänge l gilt das oben Bemerkte. Wird der Druckstab ungefähr in seiner Mitte von einem Zugstabe gekreuzt und ist er mit diesem verbunden, so wird bei steif ausgebildetem oder entsprechend kräftig gespanntem Zugstabe das Tragvermögen der Druckstrebe beträchtlich erhöht, und diesem Umstande kann dadurch Rechnung getragen werden, daß die freie Knicklänge vermindert angenommen und etwa gleich der halben Stablänge gesetzt wird. – Eingehendere theoretische Untersuchungen hierüber in [1] und insbesondere [2].

Die direkte Ermittlung der notwendigen Querschnittsfläche eines Druckstabes hat sowohl bei Zugrundelegung der Formel 1 wie der Formel 2 seine Schwierigkeit, da in diesen Formeln nebst der Fläche F auch das Trägheitsmoment J erscheint. Eine direkte Auflösung wird jedoch möglich, wenn man nach dem Vorgange Asimonts J = δ · F² setzt, worin δ ein Koeffizient ist, der wesentlich von der Querschnittsform, nicht aber von der Größe des Querschnitts abhängt. Mit Benutzung der Navierschen Formel erhält man alsdann

Die Koeffizienten δ haben Steiner [3] und Thullie [4] für die üblichen Querschnittsformen der Druckstäbe berechnet.

Die Versuche über Knickfestigkeit, die zuerst in größerem Maßstabe von amerikanischen Ingenieuren [5], [6] angestellt, dann aber namentlich von Bauschinger [7], Considéré [8] und Tetmajer [9] durchgeführt wurden, haben deutlich erwiesen, daß die empirische (Naviersche) Formel mit. den Versuchsergebnissen keine befriedigende Uebereinstimmung zeigt, wenn, wie üblich, der Knickungskoeffizient α für alle Stäbe gleichgroß angenommen wird. Dagegen kann die theoretische (Eulersche) Knickfestigkeitsformel als praktisch zutreffend angesehen werden, solange man es mit entsprechend schlanken Stäben zu tun hat, d.h. mit Stäben, für die das Verhältnis Fl²/J = l²/r², unter

den kleinsten Trägheitshalbmesser des Strebenquerschnitts verstanden, nicht unter eine gewisse Grenze herabgeht. Nach Tetmajer liegt diese Grenze für Schmiedeeisen bei l/r > 110 und wäre entsprechend der Eulerschen Formel für Schweiß- und Flußeisen im Mittel die zulässige Knickungsbeanspruchung zu setzen: s_k = 5520 (r/l)²s. Für weniger schlanke Stäbe, nämlich für ein Längenverhältnis l/r = 15–110, empfiehlt Tetmajer [10] auf Grund seiner Versuche die Formel s_k = (0,82–0,0032 l/r) · s. Dieselbe Formel, nur mit etwas geänderten Koeffizienten, entwickelt auch Jasinski [2], während ihre theoretische Begründung zuerst von Engesser gegeben wurde [11]. Gegenwärtig stehen für Schmiedeeisenkonstruktionen wohl zumeist diese Formeln von Tetmajer in Anwendung. Alle diese Regeln zur Bestimmung der zulässigen Inanspruchnahme der Druckstäbe setzen aber voraus, daß die Druckkraft in der Achse des Stabes wirkt, d.h. daß der Stab zentrisch belastet ist. Ist diese Bedingung nicht erfüllt, was beispielsweise bei einseitigem oder exzentrischem Strebenanschlusse der Fall ist, so ist die Beanspruchung des Stabes eine bedeutend ungünstigere. Regeln für die Dimensionierung solcher exzentrisch belasteter Stäbe auf Grund von Versuchen stellt Ingenieur Préaudeau auf [12].

Eingehende Versuche über das Problem der Zerknickung unter Berücksichtigung vorhandener Anfangsexzentrizität sind in neuester Zeit von Kirsch durchgeführt worden [13]. Derselbe findet bei einer vorhandenen Anfangsexzentrizität ε, einem Stabquerschnitt F, einer Länge l, einem Trägheitsradius r, einem Schlankheitsverhältnis l/r = n und einem Elastizitätskoeffizienten E die Knicklast:

worin σ_p = Maximalspannung (Proportionalitätsgrenze), e = Abstand der äußersten Faser; die maximale Spannung σ_p berechnet sich aus:

[139] Was die Querschnittsformgebung der Druckstäbe betrifft, so ist wegen der Knickungsbeanspruchung bei gegebener Fläche ein möglichst großes Trägheitsmoment bezüglich der Schwerachsen parallel und senkrecht zur Trägerwand anzustreben. Einfache Walzeisen (L- und ⊥-Eisen) werden nur für geringe Druckkräfte und kurze Längen genügen. Die auf Druck beanspruchten Gitterstäbe eines Fachwerksträgers werden zumeist aus Winkeleisen allein oder in Verbindung mit Flacheisen zusammengesetzt.

Die üblichsten Querschnittsformen, deren Wahl übrigens auch von der Querschnittsform der Gurte abhängt, sind:

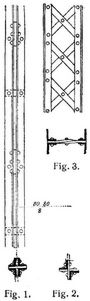
1. Der kreuzförmige Querschnitt (Fig. 1) aus vier Winkeleisen, die mit oder ohne Einschubbleche miteinander durch Nietung verbunden sind. Schwache Druckstreben werden zuweilen auch bloß aus zwei Winkeln gebildet (Fig. 2), jedoch ist hier eine gute (nicht zu weite) Vernietung mit Hilfe eingeschobener Flacheisenstücke notwendig.

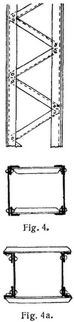
2. Der 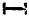-förmige Querschnitt, aus vier Winkeleisen gebildet, mit einem dazwischenliegenden vollen Stehblech oder häufiger bloß mit. einer Verbindung durch Flacheisengitter (Fig. 3), häufigst angewendete Ständerkonstruktion für Fachwerksträger von größerer Spannweite. Um die Knickfestigkeit in der Ebene der Tragwand zu sichern, werden ungleichschenklige Winkeleisen verwendet oder es wird die Breite durch aufgenietete Flacheisen vergrößert.

3. Der doppelte ]-förmige Querschnitt entweder aus zwei Walzeisen oder häufiger aus Blechen und Winkeleisen gebildet (Fig. 4). Dieser Querschnitt besitzt in beiden Achsenrichtungen ein verhältnismäßig großes Trägheitsmoment. Die beiden Stabhälften stehen so weit voneinander ab als die Stehbleche der Doppelgurte, an die sie angeschlossen sind, und sind miteinander wieder durch ein aus Flacheisen oder schwachen Winkeln gebildetes Gitterwerk verbunden. Damit diese Gitter der Erneuerung des Anstriches im Innern des Stabes nicht hinderlich sind, darf man mit der Maschenweite unter ein bestimmtes Maß nicht herabgehen. Je nachdem die Befestigung an der Außen- oder Innenseite der Gurtstehbleche erfolgt, kommt entweder die Form Fig. 4 oder Fig. 4a zur Anwendung [14].

4. Für große Kräfte, wie sie in den Endständern größerer Fachwerksträger auftreten, kommen dann noch mehr zusammengesetzte 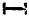-förmige oder kastenförmige, aus Blechen und Winkeleisen gebildete Querschnitte zur Anwendung.

5. Wenig üblich sind jetzt die aus Quadrant- oder Sextanteisen zusammengesetzten röhrenförmigen Druckstäbe. Dieselben waren aber in Nordamerika eine Zeitlang eine typische Konstruktion, und zwar nach den Ausführungen der Phönixville Bridge Co. (Verbindung der Segmenteisen durch Nietung) und der Keystone Bridge Co. (Verbindung durch aufgeschobene schwalbenschwanzförmige Nuteisen). Vereinzelte Anwendung hat der aus Blechen gebildete röhrenförmige Querschnitt für die Druckstäbe der Firth-of-Forth-Brücke gefunden.

Literatur: [1] Ritter, Fr., Ueber die Druckfestigkeit stabförmiger Körper mit besonderer Rücksicht auf die im steifen Fachwerk auftretenden Nebenspannungen, Schweizer. Bauztg. 1884, Nr. 7–9. – [2] Jasinski, F., Recherches sur la flexion des pièces comprimées, Annales des ponts et chaussées 1894, September; ferner Schweizer. Bauztg. 1895, S. 15, 24, 88. – [3] Handbuch der Ingen.-Wissensch., Bd. 2, Abt. 2, S. 361. – [4] Wochenschr. d. österr. Ingen.- u. Arch.-Vereins 1890, Nr. 8; 1891, Nr. 2 u. 3; 1892, Nr. 50 u. 51. – [5] Lovett, Thom. D., Report on the progress of work etc. of the Cincinnati-S.-R., Cincinnati 1875; Winkler, E, Civilingen., XXIV. – [6] Transactions of the Am. Soc. of Civ. Eng. 1882; Melan, Wochenschr. d. österr. Ingen.-Vereins 1882, Nr. 14. – [7] Mitteilungen aus dem mechanisch-technischen Laboratorium der Kgl. Techn. Hochschule München, Nr. 18, Heft 15, 1877. – [8] Mémoire sur la résistance des pièces comprimées par M. Considéré, enthalten in den Comptes rendus du Congrès international des procédés de construction, Paris 1889. – [9] Mitteilungen der Anstalt zur Prüfung von Baumaterialien am Eidgen. Polytechnikum in Zürich, Zürich 1890, Heft 4, S. 144. – [10] Schweizer. Bauztg. 1893, Bd. 22, Nr. 8. – [11] Ueber Knickfestigkeit gerader Stäbe, Zeitschr. d. Arch.- u. Ingen.-Vereins Hannover 1889 und Zeitschr. d. österr. Ingen.-Vereins 1893. – [12] Annales des ponts et chaussées 1894, Bd. 1, S. 498. – [13] Kirsch, B., Studien über das Problem der Zerknickung, Mitteilungen des k. k. Technolog. Gewerbemuseums in Wien, 1904, Heft 4. – [14] Häseler, E., Der Brückenbau, Braunschweig 1900.

(Melan) Horowitz.

Fig. 1., Fig. 2., Fig. 3.

Fig. 4., Fig. 4a.