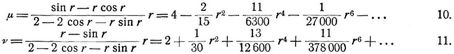Nebenspannungen

Nebenspannungen. Die statische Berechnung der Ingenieurkonstruktionen pflegt von Voraussetzungen auszugehen, die nicht vollständig erfüllt werden. Man nimmt Auflager (s.d.) als frei drehbar oder frei verschiebbar an, bei welchen Reibung stattfindet, denkt sich Kräfte in Stabachsen oder Trägerebenen wirken, auch wenn dies nicht genau zutrifft, setzt die Zwischenträger bei Berechnung der Hauptträger als frei aufliegend voraus, selbst wenn ihre Enden festgenietet sind u.s.w. Die Spannungen (Beanspruchungen pro Flächeneinheit), die sich unter diesen anfänglichen Voraussetzungen der statischen Berechnung ergeben, heißen Grundspannungen (früher Primärspannungen), während diejenigen Spannungswerte, die infolge von Abweichungen der Wirklichkeit gegen jene Voraussetzungen zu den Grundspannungen treten, Nebenspannungen genannt werden (früher Sekundärspannungen). Das Bereich der Nebenspannungen kann hiernach je nach den Voraussetzungen der statischen Berechnung etwas verschieden ausfallen. Bei Gültigkeit des Prinzips der Koexistenz elastischer Bewegungen (s.d., Bd. 5, S. 543) lassen sich für gegebene Einwirkungen zunächst die Grundspannungen für sich und alsdann die entsprechenden Nebenspannungen berechnen und durch Addition dieser beiden Anteile die Gesamtspannungen erhalten. Zu den Grundspannungen können außer den vertikalen Latten auch Winddruck, Zentrifugalkräfte, Temperaturänderungen u.s.w. beitragen. Vgl. Zusatzspannungen und [19].

Die gewöhnlichste Art von Nebenspannungen sind die Biegungsspannungen gerader Stäbe durch axial vorausgesetzten Druck (s. Knickfestigkeit), doch fanden diese bereits eingehende[595] Behandlung lange bevor man andre Nebenspannungen untersuchte oder auch nur diesen Namen anwendete. Man pflegt deshalb bei letzterem nicht in erster Linie an die gewöhnlichen Knickspannungen einzelner für sich betrachteter Druckstäbe zu denken. Wichtige Nebenspannungen können jedoch je nach der Art des Zusammenhanges der Druckstäbe mit der übrigen Konstruktion auftreten, insbesondere für die Druckgurten offener Brücken (ohne Querverband der Druckgurten), indem deren Knotenpunkte sich keineswegs als Festpunkte ansehen lassen [18], [19], S. 141, [26]. – Die Verfolgung weiterer Nebenspannungen drängte sich auf im Anschluß an die Theorie der Fachwerke (s.d.). Gebräuchliche Voraussetzungen derselben sind (vgl. Bd. 3, S. 535): a) Die Stabachsen, die an einer Verbindungsstelle (einem Knoten) zusammentreffen, schneiden sich in einem Punkte, dem Knotenpunkte daselbst; b) alle äußeren Kräfte (s.d.), mit Einschluß des Eigengewichtes, greifen in Knotenpunkten an oder wirken in Stabachsen; c) die Verbindungen sind als reibungslose Gelenke um die Knotenpunkte aufzufassen. – Unter diesen Voraussetzungen wirken die resultierenden Stabkräfte S in den Verbindungsgeraden der Knotenpunkte, die Grundspannungen sind für alle Elemente eines Stabquerschnitts F von gleichem Werte S/F (für homogenes Material und Sicherheit gegen Ausbiegung), bei prismatischen Stäben mit nur an den Enden angreifenden äußeren Kräften auch für alle Elemente beliebiger Querschnitte. Die Zugkräfte und Druckkräfte S haben jedoch Verlängerungen und Verkürzungen der Stäbe zur Folge, mit welchen bei gerade bleibenden Stäben im allgemeinen Aenderungen der Winkel zwischen letzteren verbunden wären. Können diese nicht eintreten, wie bei Anwendung von Knotennietungen anstatt der unter c) vorausgesetzten reibungslosen Gelenke, so müssen die Stäbe Biegungen erleiden, womit zu den Grundspannungen S/F die von den Biegungsmomenten herrührenden Nebenspannungen treten ([1], [2], [5], [6], [8], [10], [13], [14], [16], [22], [38], [40] u.s.w.). Diese werden auch durch Anwendung von Knotengelenken nicht vollständig vermieden, da sich letztere nicht reibungslos herstellen lassen (vgl. [9]). – Da das Eigengewicht im Gegensatz zu Voraussetzung b) nicht nur in den Knotenpunkten angreift, so können bei nicht vertikalen Stäben weitere Biegungen und entsprechende Nebenspannungen entstehen ([19], II, S. 71, [31], [39]), die bei größeren Stablängen zu beachten sind und dann auch mehrfach in Rechnung gezogen wurden (Zentralbl. der Bauverwaltung 1890, S. 176). In manchen Fällen, z.B. bei unteren Windverbänden, suchte man sie durch Zwischenunterstützungen zu vermindern. Noch größere Nebenspannungen wegen Nichterfüllung der Voraussetzung b) treten ein, wenn in nicht vertikalen Stäben auch Verkehrslasten zwischen den Knotenpunkten angreifen ([19], II, S. 71). – Wollte man die Voraussetzung a) bei Fachwerkträgern außer acht lassen, so könnten ebenfalls bedeutende Nebenspannungen die Folge sein (vgl. Druck, exzentrischer; [16], S. 188; [19], II, S. 67, [27]). Nebenspannungen infolge exzentrischer Kräfte entstehen ferner, wenn bei eben vorausgesetzten Trägern (s.d.) die Stabachsen gewisser Glieder außerhalb der Trägerebene bleiben, wie dies z.B. bei einseitiger Verbindung von Füllungsgliedern mit den Gurtungen zutrifft (vgl. Nietverbindungen und Zug, exzentrischer, sowie [11]; [17], S. 76; [19], II, S. 100; [21]; [32], [34]). – Außer den bereits berührten Nebenspannungen können bei Fachwerken selbstverständlich noch andre vorkommen, so z.B. infolge unbeabsichtigter Widerstände an den Auflagern ([19], I, S. 35, und II, S. 80), infolge der Verbindung sich kreuzender Füllungsglieder ([2], S. 293, 327; [17], S. 77; [19], S. 133; vgl. Gitterträger), infolge der Vernietung von Querträgern und Konsolen mit den Hauptträgern u.s.w. (s. [15], S. 369; [19], II, S. 81, 83, 131, 141; [20]). Wie für die Hauptträger, so können auch für die Zwischenträger, Längs- und Querverbände Nebenspannungen in Betracht kommen ([19], II, S. 32, 49, 70, 104; [29], [32]).

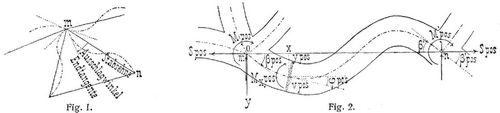
Aus dem Gesagten geht hervor, daß eine genügende Beurteilung der in einer Konstruktion auftretenden Nebenspannungen nur im einzelnen Fall, bei Kenntnis aller Verhältnisse, möglich ist, wenn auch eine Reihe nützlicher Hinweise und Ableitungen für die gewöhnlichen Anordnungen im voraus gegeben werden können [19]. Zur Berechnung der Nebenspannungen infolge der Anordnung von Knotennietungen bei bekannten Stabquerschnitten hat zuerst Manderla ein Verfahren abgeleitet [1], das für beliebige statisch bestimmte und statisch unbestimmte ebene Fachwerke anwendbar ist. Da die fraglichen Nebenspannungen besonders interessieren und am meisten untersucht wurden, so soll der allgemeine Gang ihrer Berechnung für den normalen Fall, daß sich die Achsen aller an einem Knoten eintreffenden Stäbe im gleichen Punkte schneiden, hier als Beispiel kurz angedeutet werden [1], [6]. Die Knotennietungen werden derart starr vorausgesetzt, daß sich die Achsen aller Stäbe bei einem Knotenpunkte m in der Trägerebene um den gleichen Winkel drehen. Da die bei m angreifenden äußeren Kräfte nach Voraussetzung b) durch den Punkt m selbst gehen, so müssen auch die mit ihnen im Gleichgewicht stehenden Biegungsmomente M der bei m eintreffenden Stäbe zusammen den Wert Null ergeben. Dies sind die Ausgangspunkte der Berechnung. Nach der Deformation mögen, wie üblich, die Verbindungsgeraden der Knotenpunkte Stabsehnen, die Richtungen der Stabachsen bei den Knotenpunkten Endtangenten und deren Winkel mit den zugehörigen Stabsehnen (Fig. 1) Ausschlagwinkel heißen. Letztere gelten als positiv, wenn sie von der[596] Stabsehne aus im Sinne der Bewegung des Uhrzeigers rechts herum beschrieben werden (Fig. 1 und 2). Die Biegungsmomente M_x beliebiger Querschnitte x eines Stabes der Länge l, bezogen auf die Fläche nach der Seite von x = 0 (Fig. 2), werden als positiv gerechnet, wenn sie wie der Uhrzeiger rechts um den Achspunkt des Querschnitts x drehen. M, M' seien die Endmomente des Stabes, d.h. die Momente M_x für x = 0 und x = l. Man kann bei beliebigen Einwirkungen (Lasten, Temperaturänderungen u.s.w.) wie folgt vorgehen, doch sind je nach Form und System der Träger mit Rücksicht auf Symmetrie, zugelassene Vernachlässigungen und andre Umstände mancherlei Vereinfachungen möglich, worüber die unten angeführte Literatur Aufschluß gibt.

A. Berechnung der Stabkräfte S (Zug positiv) und der Grundspannungen S/F für die in Frage stehenden Einwirkungen unter Voraussetzung reibungsloser Knotengelenke nach bekannten Methoden (s. die Art. Fachwerke, statisch bestimmte und statisch unbestimmte, Balkenfachwerke, Bogenfachwerke, Parallelträger u.s.w.).

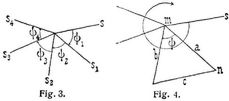
B. In jedem Knotenpunkte m (Fig. 3) von einem beliebig gewählten Stabe s ausgehend (diese s gewöhnlich Gurtungsstäbe) Berechnung der Aenderungen Δψ, welche die Winkel zwischen den Stabsehnen gegen die entsprechenden Winkel ψ vor der Deformation aufweisen. Ist ψ der im Bewegungssinne des Uhrzeigers beschriebene Winkel zwischen benachbarten Stäben der anfänglichen Längen a, b und der anfänglichen Endenentfernung c (Fig. 4), so hat man für beliebige kleine Aenderungen Δ a, Δ b, Δ c von a, b, c mit D = a b sin ψ:

Für jeden Stab l vom Querschnitt F, Elastizitätsmodul E und Ausdehnungskoeffizienten α entspricht einer Beanspruchung S und Temperaturänderung τ die Längenänderung:

Wenn also a, b, c Stäbe sind, läßt sich nach 1. Schreiben:

worin die Indices andeuten, auf welche Stäbe sich die Klammerausdrücke beziehen. Gelten für die drei Stäbe a, b, c gleiche α τ wie in dem gewöhnlichen Falle gleicher Temperaturänderungen bei gleichem Material, dann wird aus 3.:

Die Temperaturänderungen haben in diesem Falle keinen Einfluß auf die betrachteten Nebenspannungen. Zur Kontrolle kann dienen, daß für die drei Winkel ψ, χ, φ des durch a, b, c gebildeten Dreiecks sein muß:

Δ ψ + Δ χ + Δ φ = 0.

5.

C. Bildung der Ausdrücke für die Ausschlagwinkel β₁, β₂, ... der Stäbe s₁ s₂, ... in den einzelnen Knotenpunkten (Fig. 1, 3):

β_n = β – Σ Δ ψ,

6.

worin β der Ausschlagwinkel des Stabes s (»Stellungswinkel« bei m) und die Summe Σ auf die unter B. berechneten Winkeländerungen Δ ψ zwischen s und dem betreffenden Stab s_n zu erstrecken sind.

D. Für jeden Knotenpunkt m Ansatz der Ausdrücke für die Endmomente M aller daselbst eintreffenden Stäbe und der für dieselben bestehenden Bedingungsgleichung:

Bezeichnet J das Trägheitsmoment des Querschnitts eines Stabes der Länge l für eine Achse senkrecht zur Trägerebene durch den Schwerpunkt des Querschnitts, so hat man die Endmomente bei x = 0 und l:

worin β, β' die unter C. erwähnten Ausschlagwinkel bei; x = 0 und l (Fig. 2) und mit

von der Stabkraft S abhängig:

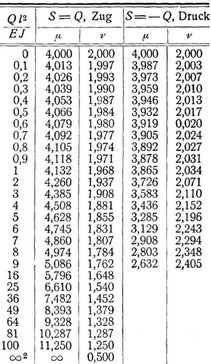
In der folgenden Tabelle sind eine Anzahl Werte von μ, ν eingetragen, die für Druck (der notwendigen größeren J wegen) zu genügen pflegen. Für Zug kann man auch setzen:

oder

[597] und für große z (etwa z > 6) mit k = 1 genügend angenähert:

μ = z(z – 1)/(z – 2), ν = z/(z – 2)

15.

E. Berechnung der Stellungswinkel β (Ausschlagwinkel der Stabes, Fig. 3) aus den Momentengleichungen 7., deren ebensoviele als Knotenpunkte, d.h. als Stellungswinkel, existieren, und der übrigen Ausschlagwinkel aus 6.

F. Berechnung der Endmomente aller Stäbe aus 8.

G. Es treten dann an den Stabenden zu den Grundspannungen S/F die von M, M' herrührenden Nebenspannungen, so daß die ganzen Normalspannungen in Entfernungen v von der Achsschicht (vgl. Bd. 1, S. 799, Formel 25.):

σ = S/F + (M/J)v, σ' = S/F + (M'/J)v,

16.

worin v positiv in der positiven Richtung der y-Achse (Fig. 2), die von der in m beginnenden positiven Richtung der x-Achse durch eine der Bewegung des Uhrzeigers entsprechende Drehung um 90° erreicht wird. Die Grenzwerte der Normalspannungen 16. treten mit den Grenzwerten von v in den äußersten Fasern ein und werden Randspannungen genannt. Die größte Randspannung σ bezw. σ' liegt auf derjenigen Seite der Achsschicht, auf der die Nebenspannung Mv/J bezw. M'v/J von gleichem Vorzeichen wie die Grundspannung S/F ist. Die größte dieser Randspannungen an den Stabenden, die durch Randspannungen in andern Querschnitten x nicht oder nur unerheblich überschritten wird, gilt als größte, Spannung des Stabes. – Beispiele der Berechnung von Nebenspannungen infolge fester Knotenverbindungen in [1], [15], [22], [38] u.s.w.

Aus der vorstehend angedeuteten Berechnung ist bereits ersichtlich, daß die Ermittlung aller erkennbaren Nebenspannungen eine weitläufige und häufig unlösbare Aufgabe wäre. Es fragt sich nun, inwieweit man die Nebenspannungen berücksichtigen soll, wobei zu beachten, daß die Voraussetzungen der Berechnung zum Teil unsicher und jedenfalls nur annähernd zutreffend sind. Bei den bisherigen Bruchversuchen mit Fachwerkträgern (vgl. Bd. 3, S. 537) haben letztere etwa so viel ausgehalten, als nach der üblichen Berechnung, d.h. ohne Berücksichtigung fester Knotenverbindungen und andrer unvermeidlichen Nebenspannungen, zu erwarten war. Dies mag daher rühren, daß mit Eintritt bleibender Formänderungen durch die größeren Spannungen eine gleichmäßigere Verteilung der Stabkräfte auf die Querschnitte stattfindet. Für die durch einseitige Belastung (ungünstigste Belastung der mittleren Füllungsglieder) bis zum Bruche erprobte Emmebrücke bei Wolhusen in der Schweiz beispielsweise (Parallelträger einfachen Systems des gleichschenkligen Dreiecks) ergab die Berechnung besonders große Nebenspannungen, da die Schwerlinien der Füllungsglieder sich nicht in den Gurtungsschwerlinien schnitten [27], S. 10. Demgemäß traten bedeutende Deformationen schon vor Aufbringen der halben Bruchlast ein. Dieselben nahmen jedoch mit wachsender Belastung in weit geringerem Maße zu, als der Berechnung entsprach, und erschienen an den ungünstigst beanspruchten Stellen selbst dann noch nicht beunruhigend, als nach der üblichen Berechnung mit Rücksicht auf Nebenspannungen der Bruch zu erwarten war [27], S. 42. Dieser trat schließlich im Einklang mit der gewöhnlichen Berechnung ohne Rücksicht auf Nebenspannungen bei einem gedrückten Füllungsgliede ein, als nach der Euler-Tetmajerschen Knickformel (Bd. 5, S. 520, 522) auf Grund einer »freien Knicklänge« von 0,732 der Stablänge zwischen den Knotenpunkten die Knickfestigkeit überschritten wurde. – Für die Bruchversuche mit der Neißebrücke bei Forst (Schwedlerträger einfachen Systems) wurde die ganze Spannweite gleichmäßig belastet (Zeitschr. für Bauwesen 1895, S/289), so daß nach der gewöhnlichen Berechnung zuerst ein Nachgeben der Gurtungen in der Brückenmitte zu erwarten war. Es fand in je einem mittleren Felde beider Träger Ausknicken der gedrückten Obergurten bei 2375 kg Grundspannung pro 1 qcm unter Zerreißen der Gitterstäbe zwischen den zwei Teilen der Gurten (Fig. 5) statt. Aus den veröffentlichten Skizzen geht hervor, daß die freie Knicklänge hierbei etwa 0,6 der Stablänge zwischen den Knotenpunkten war. Berechnet man demgemäß die Knickfestigkeit auf Grund der Tetmajerschen Formel für Schweißeisen (Bd. 5, S. 522), so zeigt sich, daß mit dem Zerreißen der ungenügenden Verbindung beider Gurtungsteile die Knickfestigkeit von 2770 auf 1740 kg und damit die Sicherheit von 2770 : 2375 = 1,17 auf 1740 : 2375 = 0,73 sank, so daß der Bruch eintreten mußte, ohne daß weitere Nebenspannungen mitgewirkt zu haben brauchen. – Auch die eingehenden Messungen mit Dehnungszeichnern u.s.w. am Oschütztalviadukt führten zu dem Schlußergebnis, daß nirgends eine unerlaubte Beanspruchung stattfand, sondern im Gegenteil viele Konstruktionsteile infolge der Mitwirkung andrer geringere Anstrengungen auswiesen, als nach der gewöhnlichen Berechnung anzunehmen war [12], S. 484. Berücksichtigt man ferner, daß bei Festsetzung der gebräuchlichen zulässigen Beanspruchungen die Nebenspannungen überhaupt noch wenig Beachtung fanden, so wird man auch in Zukunft nicht alle Nebenspannungen für die Dimensionierung im einzelnen zu berechnen brauchen.

[598] Werden die Grenzwerte der Beanspruchungen auf Grund der ungünstigsten Belastungen festgestellt und die weiter auftretenden Einwirkungen in gebräuchlicher Weise berücksichtigt (Winddruck, Temperaturänderungen bei Bogen u.s.w., s. Zusatzspannungen), so dürfte es meist genügen, folgende Quellen von Nebenspannungen bei der Berechnung in Betracht zu ziehen: 1. Knickwirkungen unter vorsichtiger Wahl der zu verwendenden Formeln und freien Knicklängen (s. Knickfestigkeit und [19], II, S. 105, vgl. Bd. 3, S. 539, und Bd. 2, S. 58) sowie besonderer Berücksichtigung der Verhältnisse offener Brücken [18], [19], II, S. 141, [26]. 2. Exzentrische Beanspruchungen, insbesondere wenn sich die Schwerlinien der Füllungsglieder außerhalb der Gurtungsschwerlinien schneiden (s. Druck, exzentrischer, und [11]; [17], S. 76; [19] II, S. 67, 100; [21], [32], [34]). 3. Belastungen außerhalb der Knotenpunkte, wenn es sich um Einzellasten handelt, oder wenn bei langen Stäben erhebliche Biegungsspannungen durch das Eigengewicht entstehen können ([19], II, S. 71). 4. Vernietung der Querträger mit den Hauptträgern, wenn die Vertikalen nicht mit Rücksicht auf Anschlüsse, Querversteifungen u.s.w. ohnehin stärker als nötig ausfallen (s. [15], S. 369; [19], II, S. 52,59, 131, 142). Außerdem können je nach Umständen Verdrehungsspannungen durch Anschluß von Konsolen an die Hauptträger und Vernietung der sekundären Längsträger mit den Querträgern sowie manche andre Nebenspannungen rechnerisch oder schätzungsweise festzustellen oder ohne Feststellung im einzelnen bei der Dimensionierung zu berücksichtigen sein ([19], II, S. 81, 83; [20]; [29], [32] u.s.w.). Ganz besonders aber kommt es darauf an, durch die Art der Konstruktion, ihre Herstellung, Aufteilung und Unterhaltung unnötige Nebenspannungen zu vermeiden und die unvermeidlichen so weit herabzusetzen, als mit der Zweckmäßigkeit und Sicherheit der Konstruktion verträglich ist (vgl. Dimensionenberechnung, Zulässige Beanspruchung).

Literatur: [1] Manderla, Die Berechnung der Sekundärspannungen, welche im einfachen Fachwerk infolge starrer Knotenverbindungen auftreten, Allg. Bauztg. 1880, S. 34. – [2] Winkler, Die Theorie der Brücken, II, Theorie der gegliederten Balkenträger, Wien 1881, S. 276, 343 (s.a. Die Querkonstruktionen der eisernen Brücken, Wien 1879, S. 170, 286). – [3] Allievi, Equilibrio interno delle pile metalliche, Rom 1882 (deutsch von Totz, Wien 1888). – [4] Ritter, Fr., Ueber die Druckfestigkeit stabförmiger Körper mit besonderer Rücksicht auf die im steifen Fachwerk auftretenden Nebenspannungen, Schweiz. Bauztg. 1884,1, S. 37, 43, 47. – [5] Manderla, Die Formänderung des Fachwerks bei wechselnder Belastung, Allg. Bauztg. 1884, S. 81, 89. – [6] Weyrauch, Aufgaben zur Theorie elastischer Körper, Leipzig 1885, S. 269. – [7] Landsberg, Ebene Fachwerke mit festen Knoten Verbindungen und das Prinzip der Deformationsarbeit, Zentralblatt der Bauverwaltung 1885, S. 165. – [8] Ders., Beitrag zur Theorie der Fachwerke, Zeitschr. d. Arch.- u. Ing.-Ver. zu Hannover 1885, S. 361; 1886, S. 195 (s.a. Festschr. der Techn. Hochschule Darmstadt 1886, S. 1). – [9] Manderla, Ueber die Wirkungsweise gelenkförmiger Knotenverbindungen, Allg. Bauztg. 1886, S. 9, 20, 32, 37. – [10] Müller-Breslau, Theorie der Biegungsspannungen in Fachwerkträgern, Zeitschr. d. Arch.- u. Ing.-Ver. zu Hannover 1886, S. 399. – [11] Considère, Note sur les effets anormaux dans les ouvrages métalliques, Annales des ponts et chaussées 1887, I, S. 372. – [12] Fränkel und Krüger, Spannungs- und Formänderungsmessungen an dem eisernen Pendelpfeilerviadukte über das Oschütztal bei Weida, Civilingenieur 1887, S. 439 (Nebenspannungen der Pfeiler S. 484). – [13] Hacker, Ueber Biegungsspannungen in Schwedlerschen Kuppeln, Zeitschr. d. Arch.- u. Ing.-Ver. zu Hannover 1888, S. 223. – [14] Engesser, Ueber die Nebenspannungen der Fachwerkstäbe bei steifen Knotenverbindungen, Zeitschr. d. Ver. deutsch. Ing. 1888, S. 813. – [15] Handb. d. Ing.-Wiss., II, Brückenbau, 2. Abt., Leipzig 1890, S. 357 (von Steiner, s.a. Tech. Blätter 1880, S. 134). – [16] Ritter, W., Anwendungen der graphischen Statik, II, Das Fachwerk, Zürich 1890, S. 171. – [17] Brik, Fachwissenschaftliche Erörterungen zu dem Berichte des Brückenmaterialkomitees über die durchgeführten Versuche mit genieteten Trägern aus Fluß- und Schweißeisen, Zeitschr. d. Oesterr. Ing.- u. Arch.-Ver. 1891, S. 76. – [18] Engesser, Die seitliche Standfestigkeit offener Brücken, Zentralblatt der Bauverwaltung 1892, S. 349. – [19] Ders., Die Zusatzkräfte und Nebenspannungen eiserner Fachwerkbrücken, I, Die Zusatzkräfte, Berlin 1892; II, Die Nebenspannungen, Berlin 1893. – [20] Barkhausen, Der Steifrahmen im Wind- und Querverbände geschlossener Trogbrücken, Zeitschr. d. Ver. deutsch. Ing. 1892, S. 421, 492. – [21] Ders., Biegungsspannungen in Blechen und Bändern infolge von einseitiger Verlaschung oder von Ueberlappungsverbindungen, ebend. 1892, S. 553. – [22] Mohr, Die Berechnung der Fachwerke mit starren Knotenverbindungen, Civilingenieur 1892, S. 577; 1893, S. 67. – [23] Jacquier, Note sur les efforts secondaires qui peuvent se produire dans les systèmes articulés à attaches rigides, Ann. des ponts et chaussées 1893, I, S. 1142. – [24] Engesser, Die zusätzlichen Beanspruchungen durchgehender (kontinuierlicher) Brückenkonstruktionen, Zeitschr. f. Bauwesen 1894, S. 305. – [25] Ders., Ueber die Verringerung der Nebenspannungen durch die Art der Aufstellung, Zentralblatt der Bauverwaltung 1895, S. 317. – [26] Ders., Ueber die Knickfestigkeit offener Brücken, Zeitschr. d. Ver. deutsch. Ing. 1895, S. 1021. – [27] Rapport sur les épreuves de Charge jusqu'à rupture de l'ancien pont sur l'Emme à Wolhusen, Bern 1895. – [28] Dupuy,[599] Pont de Cosne, Comparaison entre le travail calculé et le travail observé, Ann. des ponts et chaussées 1895, II, S. 461. – [29] Häseler, Berechnung der auf Verdrehung beanspruchten Brückenquerträger, Zeitschr. d. Ver. deutsch. Ing. 1896, S. 761. – [30] Dupuy, Résistance des barres soumises à des efforts agissant parallelement à leur axe neutre et en dehors de cette axe, Ann. des ponts et chaussés 1896, II, S. 223 (s.a. Mesnager, S. 750). – [31] Tolle, Die steife Kettenlinie, Zeitschr. d. Ver. deutsch. Ing. 1897, S. 855 (Zwischenaufhängung horizontaler und geneigter Zugstangen). – [32] Häseler, Der Brückenbau, I, Die eisernen Brücken, 3. Lief., Braunschweig 1897, S. 339; 4. Lief., Braunschweig 1900, S. 492, 571. – [33] Franke, Berechnung der Durchbiegung und der Nebenspannungen von Fachwerkträgern, Zeitschr. für Bauwesen 1898, S. 111. – [34] Weyrauch, Ueber exzentrische Zugbeanspruchung von Fachwerkstäben, Zeitschr. für Architektur und Ingenieurwesen, Wochenausg. 1899, S. 250. – [35] Propst, Einiges über Gelenke massiver Bogenbrücken, ebend., Wochenausg. 1899, S. 546. – [36] Mörsch, Nebenspannungen in Brückengewölben mit drei Gelenken, ebend. 1900, S. 193. – [37] Engesser, Einfluß der Nebenspannungen auf die Durchbiegung der Fachwerkträger, ebend. 1900, S. 533. – [38] Patton, Beitrag zur Berechnung der Nebenspannungen infolge starrer Knotenverbindungen bei Brückenträgern, ebend. 1902, S. 417 (Beispiele). – [39] Häseler, Beanspruchung und Streckung der Winddiagonalen infolge Durchhängens, Zeitschr. d. Ver. deutsch. Ing. 1902, S. 686. – [40] Jordan, Ueber die Berechnung der Nebenspannungen in Fachwerken mit steifen Knotenverbindungen (Dissertation), Straßburg 1904, – S. ferner Knickfestigkeit, Druck, exzentrischer, Zug, exzentrischer; Gitterträger, Dimensionenberechnung, Zusatzspannungen.

Weyrauch.

Fig. 1., Fig. 2.

Fig. 3., Fig. 4.

Fig. 5.