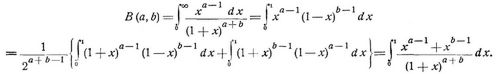- Gammafunktionen
Gammafunktionen (Eulersche Integrale), eine wichtige Klasse bestimmter Integrale.
Eulersches Integral erster Gattung oder Betafunktion (s.d.), das Integral
Es ist B (a, b) = B (b, a). Für ganzzahlige positive a und b ist B (a, b) = 1 · 2 · 3 ... b – 1/a (a + 1) (a + 2)... (a + b – 1)
Eulersches Integral zweiter Gattung oder Gammafunktion, das Integral
Vermittelst dieser Funktion ist B (a, b) = Γ(a) Γ(b)/Γ(a + b). Ferner ist
also für positive ganzzahlige a:
Weiter ist
Man braucht daher die Werte von Γ(a) nur zwischen a = 0 und a = 1/2[255] zu kennen. Sodann ist
Es ist
Die Gammafunktion ist stetig.
Légendresches Theorem:
Die Funktion Γ(a) erreicht für a = 1,4616 ..., den kleinsten Wert 0,8856 ... Für große Werte von a berechnet man die Gammafunktion aus der halbkonvergenten Stirlingschen Formel:
wo B1 B2 ... die Bernoullischen Zahlen sind. Tabelle findet sich in [4].
Literatur: [1] Serret, Lehrbuch der Integralrechnung, deutsch von A. Harnack, Leipzig 1885, 1. Hälfte, Kap. 3. – [2] Meyer, G.F., Vorlesungen über die Theorie der bestimmten Integrale, Leipzig 1871, S. 88–157. – [3] Schobloch, J.A., Ueber Beta- und Gammafunktionen, Halle 1884. – [4] Légendre, Traité des fonctions elliptiques et des intégrales Eulériennes, Bd. 2, Paris 1825–32. – [5] Brunel, G.E. A., Monographie de la fonction Gamma, Bordeaux 1886. – [6] Godefroy, M., La fonction Gamma, Paris 1901. – [7] Graf, J.H., Einleitung in die Theorie der Gammafunktionen und der Eulerschen Integrale, Bern 1894. – [8] Nielsen, N., Handbuch der Gammafunktion, Leipzig 1906.
Wölffing.
http://www.zeno.org/Lueger-1904.