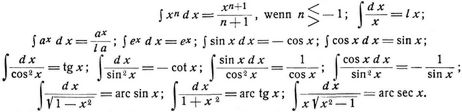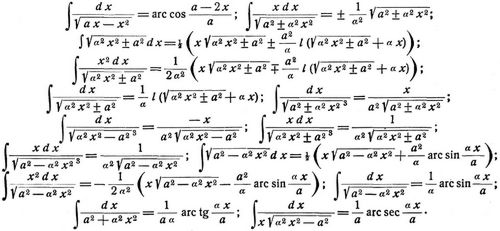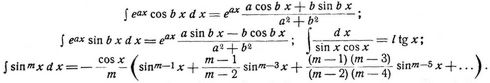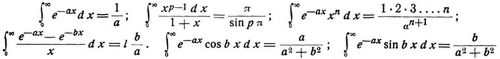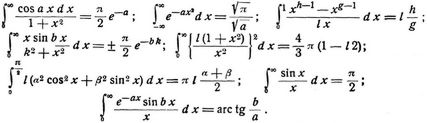Integralrechnung

Integralrechnung ist die umgekehrte Operation der Differentialrechnung. Eine Funktion F(x) ist Integral der Funktion f(x) und wird mit f(x) d x bezeichnet, wenn d F (x)/d x = f (x) ist; f(x) heißt Integrand.

A. Unbestimmte Integrale.

Weil die Ableitung einer Konstanten Null ist, so ist jedes Integral nur bis auf eine additive Konstante (die sogenannte willkürliche Konstante) bestimmt: es ist F(x) = ∫ f(x) d x + C.

a) Grundregeln der Integralrechnung. Es ist ∫ a f(x) d x = a ∫ f(x) d x, ferner

∫ [ f(x) ± φ(x)] d x = ∫ f(x) i x ± ∫ φ (x) d x.

b) Fundamentalformeln.

c) Allgemeine Hilfsmittel und Reduktionsformeln der Integralrechnung.

α) Einführung neuer Veränderlichen, z.B.

gibt mit x = z – a:

So ergeben sich die Formeln:

ß) Teilweise Integration. Es ist ∫ u d v = u v – ∫ v d u. Beispiel ∫ l x d x : u = l x; d v = d x; d u = d x/x; v = x; also ∫ l x d x = x l x – ∫ x d x/x = x (l x – 1). Ebenso erhält man

[200] γ. Einige häufiger vorkommende Integralformeln.

δ) Integration durch Reihenentwicklung, wenn andre Hilfsmittel vertagen.

d) Integration rationaler Funktionen. Eine rational gebrochene Funktion muß in Partialbrüche zerlegt werden. Ist zu berechnen

und ist a eine Wurzel von F(x) = 0, so ist der zugehörige Partialbruch A/x – a, wo A = f(a)/F(a). Hat F(x) = 0 zwei komplex konjugierte Wurzeln, so bleiben die zugehörigen Partialbrüche vereinigt:

Im Nenner wird durch die Substitution y = √γ x + c/√γ die Summe zweier Quadrate hergestellt:

Ist a eine r-fache Wurzel von F(x) = 0, so lautet die Partialbruchzerlegung A/x – a + A₁/(x – a)² + A₂/ (x – a)³ + ... + A_r–1/(x – a)^r.

e) Integration irrationaler Funktionen.

α) Eine Wurzel aus einem linearen Ausdruck

ist unter dem Integralzeichen vorhanden. Der Integrand wird durch die Substitution

rational gemacht.

ß) Der Integrand ist eine rationale Funktion von x und R, wo

so daß also zu berechnen

weil R² in x rational ist (f₁ φ₁ F₁ Φ₁ sind rationale ganze Funktionen von x). Man macht den Nenner rational:

Der erste Teil dieses Integrals ist rational; im zweiten Teil bringt man R wieder in den Nenner:

Die Funktion φ(x)/F(x) wird zerlegt in eine ganze rationale Funktion f(x) und eine Summe S von Partialbrüchen.

¹) In dem Integral

wird der Ausdruck unter dem Wurzelzeichen durch eine lineare Substitution auf die Summe oder Differenz zweier Quadrate gebracht. Ist γ positiv, so setzt man

ist γ negativ,

Dann wird das Integral:

und wenn man in Φ (y) die geraden und ungeraden Potenzen von y trennt, geht dasselbe über in

Das erste Integral wird durch z = y² rational. Die Glieder des zweiten haben die Form:

und reduzieren sich vermittelst der Formel:

auf das Integral

(s. oben A c γ).

Man kann auch für das Integral

wo X vom nten Grade ist, den Wert[201] anschreiben:

und erhält durch Ableiten des Integrals und seines Wertes und Koeffizientenvergleichung n + 1 Gleichungen für die unbestimmten Koeffizienten A₀, A₁, ..., A_{n – 1}, B.

²) Ein Partialbruch von S liefert ein Integral ∫d x/[(x – α)R]. Durch die Substitution y = 1/(x – α) kommt man auf einen Integranden, in dessen Nenner nur eine Quadratwurzel steht, also auf den Fall A e β 1 zurück. Ebenso verfährt man auch, wenn F (x) = 0 eine mehrfache Wurzel hat und daher ein Integral ∫d x/[(x – α)^rR] vorliegt. Hat F (x) = 0 zwei komplex-konjugierte Wurzeln, so vereinigt man die betreffenden Partialbrüche und erhält

Man setzt nun x = (M ξ+ N)/(ξ + 1) und bestimmt M und N so, daß im Nenner unter dem Wurzelzeichen und außerhalb desselben die Glieder mit ξ wegfallen. Das Integral wird damit:

Im ersten Integral hat man schließlich √(γ₁ ξ² + C₁) = ζ, im zweiten √(γ₁ ξ² + C₁) = ξ/ζ zu setzen, um sie rational zu machen.

γ) Zwei Quadratwurzeln je aus einem linearen Ausdruck kommen auf den Fall β zurück.

δ) Eine Quadratwurzel aus einem Ausdruck dritten oder vierten Grads führt auf elliptische Integrale (s.d.); eine Ausnahme bilden jedoch die sogenannten pseudoelliptischen Integrale, bei welchen man mit algebraischen, logarithmischen und cyklometrischen Funktionen auskommt, z.B.

kommt mit x² = ξ auf den Fall A, e, β zurück.

f) Transzendente Integrale. Beispiele von solchen sind

Das letzte Glied ist entweder

je nachdem m gerade oder ungerade.

Viele Integrale von trigonometrischen Funktionen können durch die Substitution t = tg x/2 rational gemacht werden. Es ist alsdann nämlich cos x = (1 – t²)/(1 + t²); sin x = 2t/(1 + t²); tg t = 2t/(1 – t²).

g) Mehrfache Integrale. Eine Funktion von zwei Veränderlichen kann der Reihe nach nach x und nach y integriert werden, wobei im ersten Fall y, im zweiten x als Konstante behandelt wird. Die Reihenfolge dieser Integrationen ist übrigens vertauschbar:

∫[∫f (x, y)d x]d y = ∫[∫f (x, y)d y]d x.

Auf diese Weise entstehen Doppel- und mehrfache Integrale.

B. Bestimmte Integrale.

Die willkürliche Konstante eines Integrals ∫f (x, y)d x = F(x) + C läßt sich dadurch bestimmen, daß das Integral für einen bestimmten Wert a von x den gegebenen Wert F(a) haben soll. Dann wird ∫f (x, y)d x = F (x) – F(a). Dieser Wert ist von x und von a abhängig. Das Integral heißt alsdann ein bestimmtes Integral und wird mit

bezeichnet; a heißt untere, x obere Grenze desselben. Dabei kann auch x einen bestimmten Wert b annehmen

Der Wert desselben ist nur von den Grenzen a und b, nicht aber von der Wahl des Integrationsbuchstabens x abhängig. Vertauschung der Grenzen bedingt Aenderung des Vorzeichens;

Durch Differentiation nach der oberen Grenze ergibt sich

also der Integrand. Auch bestimmte Integrale mit unendlich großen Grenzen und solche, deren Integrand an den Grenzen unstetig wird, können endliche Werte besitzen. Auf Unstetigkeitsstellen des Integranden zwischen den Grenzen muß Rücksicht genommen werden. Näheres s. [1], S. 91–94.

In vielen Fällen lassen sich bestimmte Integrale zwischen gewissen Grenzen in geschlossener Form (d.h. durch bekannte Funktionen) darstellen, während dies bei dem betreffenden[202] unbestimmten Integral nicht möglich ist. Als Hauptmethode dient hierzu die Differentiation und Integration bekannter Integrale nach einer von den Grenzen unabhängigen, im Integranden vorkommenden Konstanten (Parameter). Denn wenn

so ist auch

und

Doch darf in bestimmten Doppelintegralen die Reihenfolge der Integrationen nur umgekehrt werden, wenn die Grenzen konstant sind.

Beispiele von häufiger vorkommenden bestimmten Integralen sind:

Ferner wenn a > b:

und

Weiter ist:

Bestimmte Integrale mit komplexen Veränderlichen s. Funktionentheorie.

C. Neue Funktionen.

Einige Integrale, welche nicht auf bekannte Funktionen führen und daher neue Funktionen definieren, sind mit besonderen Namen belegt worden: a) Integrale mit veränderlichen oberen Grenzen: z.B. der Integrallogarithmus

das Exponentialintegral

das Sinusintegral

das Cosinusintegral

b) Bestimmte Integrale mit konstanten Grenzen, welche Funktionen eines im Integranden auftretenden Parameters sind: z.B. die Beta-, Gamma-, Kugel-, Zylinderfunktionen, die Fourierschen Integrale.

D. Anwendungen der Integralrechnung.

Flächenbestimmung (s. Quadratur) bei den ebenen Kurven Bogenmessung (s. Rektifikation) bei den ebenen und räumlichen Kurven, Inhaltsbestimmung (s. Kubatur) und Oberflächenmessung (s. Komplanation) bei den Flächen; ferner Bestimmung von Schwerpunkten, Massen- und Trägheitsmomenten, Potentialen u.s.w. in der Mechanik und mathematischen Physik.

Literatur: Von den angeführten Werken sind [1] und [2] besonders zum Studium zu empfehlen; [5], [6] und [15] behandeln die bestimmten Integrale; [7] ist ein empfehlenswertes kleines Repetitionsbuch; [8]–[10] sind Uebungsbücher. Die geometrischen Anwendungen behandelt [11], die naturwissenschaftlichen [12], die technischen [13]. – [1] Serret, Lehrbuch der Differential- und Integralrechnung, deutsch von Harnack, 2. Aufl., Bd. 2, Leipzig 1899. – [2] Stegemann-Kiepert, Grundriß der Differential- und Integralrechnung, II. Integralrechnung, 9. Aufl., Hannover 1903. – [3] Picard, Traité d'analyse, Bd. 1, Paris 1904. – [4] Meyer, G.F., Vorlesungen über die Theorie der bestimmten Integrale, Leipzig 1871. – [5] Bierens de Haan, Exposé de la théorie des intégrales définies, Amsterdam 1862. – [6] Kronecker, Vorlesungen über die Theorie der einfachen und vielfachen bestimmten Integrale, herausg. v. Netto, Leipzig 1894. – [7] Deter, Repetitorium der Differential- und Integralrechnung, 4. Aufl., Berlin 1899. – [8] Dölp, H., Aufgaben zur Differential- und Integralrechnung, 10. Aufl., Gießen 1903. – [9] Schlömilch, O., Uebungsbuch zum Studium der höheren Analysis, 4. Aufl., Bd. 2, Leipzig 1900. – [10] Sohncke, Aufgaben aus der Differential- und Integralrechnung, 6. Aufl., Jena 1905–06. – [11] Joachimsthal, Anwendung der Differential- und Integralrechnung auf die allgemeine Theorie der Flächen und der Linien doppelter Krümmung, herausg. von Natani, Leipzig 1890. – [12] Fuhrmann, A., Naturwissenschaftliche Anwendungen der Integralrechnung, 2. Aufl., Berlin 1903. – [13] Ders., Bauwissenschaftliche Anwendungen der Integralrechnung, Berlin 1903. – [14] Meyer, F.W., Integralrechnung, Leipzig 1905. – [15] Lejeune-Dirichlet, Vorlesungen über die Lehre von den einfachen u. mehrfachen bestimmten Integralen, Braunschweig 1904.

Wölffing.