Gliederpaare

Gliederpaare, Beweglichkeit. Die Beweglichkeit zweier Glieder wird durch die Flächenteile benimmt, in denen sich diese Glieder während ihrer gegenseitigen Bewegung beständig berühren; und zwei solche zusammengehörige Glieder bilden ein Gliederpaar.

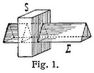
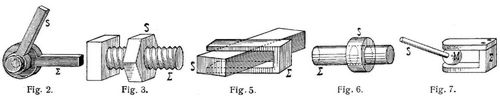
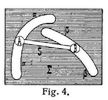
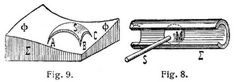
Gleitet in Fig. 1 ein Glied S mit den Seitenflächen eines Hohlprismas auf den entsprechenden Seitenflächen eines Vollprismas Σ, so bewegen sich die Punkte des Gliedes S in bezug auf das Glied Σ in Geraden, die zu den Prismakanten parallel sind; und ebenso bewegen sich umgekehrt die Punkte des Gliedes Σ in bezug auf das Glied S. Bei diesen beiden Gliedern, welche sich in Prismaflächen berühren, entsteht eine geradlinige Parallelbewegung, und die gegenseitige Bewegung ist geradlinig. – Dreht sich in Fig. 2 ein Vollzylinder des Gliedes S in dem entsprechenden Hohlzylinder des Gliedes Σ, dann beschreiben die Punkte des Gliedes S, welche nicht in der gemeinsamen Achse beider Zylinder liegen, in bezug auf das Glied Σ Kreise, deren Ebenen senkrecht zu dieser Achse sind und deren Mittelpunkte in derselben liegen. Dasselbe gilt von der Bewegung der Punkte des Gliedes Σ in bezug auf das Glied S. Bei diesen beiden Gliedern, die sich in Zylinderflächen oder statt dessen auch in koaxialen Rotationsflächen berühren, entsteht eine kreislinige Bewegung. Die gegenseitige Bewegung dieser beiden Glieder, die ein Achsengelenk bilden, ist kreislinig. – Bei einer Schraubenmutter S auf einer Schraube Σ in Fig. 3 beschreiben alle Punkte des Gliedes S koaxiale Schraubenlinien von gleicher Ganghöhe in bezug auf das Glied Σ und umgekehrt. Nur die Punkte, die in der Schraubenachse liegen, bewegen sich in derselben und beschreiben also eine Gerade, die als eine Schraubenlinie vom Radius gleich Null betrachtet werden kann. Diese Glieder berühren sich in Schraubenflächen, und ihre gegenseitigen Bewegungen sind schraubenlinig. – Die drei betrachteten Gliederpaare zeichnen sich dadurch aus, daß ein Punkt des einen Gliedes und ein Punkt des andern Gliedes, die in einer Lage koinzidieren, dieselbe Bahn beschreiben. Die Bewegung von S in bezug auf Σ und umgekehrt von Σ in bezug auf S ist dieselbe. Bewegen sich die Punkte eines Gliedes in bezug auf ein andres in bestimmten Bahnen, dann ist die Beweglichkeit linienläufig und wird auch zwangläufig genannt. – Gleiten in Fig. 4 die zylindrischen Zapfen A B eines Gliedes S bezw. in den Nuten α, β, eines plattenförmigen Gliedes Σ, dann beschreiben alle Punkte des Gliedes S bestimmte ebene Kurven gegen das Glied Σ; und ebenso beschreiben auch die Punkte des Gliedes Σ bestimmte ebene Kurven gegen das Glied S. Diese Kurven sind aber von jenen Kurven verschieden. Die Zylinderflächen der Zapfen und die Zylinderflächen der Nuten berühren sich während der Bewegung dieser beiden Glieder S, Σ. Ihre gegenseitige Beweglichkeit ist kurvenläufig oder zwangläufig; aber die Beweglichkeit ist verschieden von S in bezug auf Σ und umgekehrt von Σ in bezug auf S. – Gleiten in Fig. 5 zwei parallele Seitenflächen des Gliedes S zwischen. den parallelen Ebenen des Einschnittes des Gliedes Σ, dann bewegen sich die Punkte des Gliedes S in parallelen Ebenen in bezug auf das Glied Σ, und umgekehrt gilt dasselbe. Die gegenseitige Beweglichkeit bei diesem Gliederpaar ist ebenenläufig. – Bei einem Hohlzylinder S auf einem Vollzylinder Σ in Fig. 6 bewegen sich die Punkte des einen Gliedes in bezug auf das andre in koaxialen Rotationszylinderflächen. Nur für die Punkte in der gemeinsamen Achse der Zylinderflächen ist die Bewegung geradlinig; und diese Achse kann als eine Rotationszylinderfläche vom Radius gleich Null betrachtet werden. Die gegenseitige Beweglichkeit dieser beiden Glieder ist zylinderflächenläufig, und ist dieselbe von einem Gliede in bezug auf das andre. – In Fig. 7 berührt die Kugel des Gliedes S in zwei entsprechenden kleinen konzentrischen Kugelhauben das Glied Σ. Die Punkte des Gliedes S bewegen sich, soweit es die Gestaltung der Glieder zuläßt, auf konzentrischen Kugelflächen. Dasselbe gilt umgekehrt für die Bewegung der Punkte des Gliedes Σ in bezug auf das Glied S.[572] Nur der gemeinsame Kugelmittelpunkt M ist unbeweglich gegen die Glieder. Bei diesem Gliederpaar, das ein Kugelgelenk bildet, ist die Beweglichkeit kugelflächenläufig und dieselbe von einem Gliede in bezug auf das andre. – In Fig. 8 berührt die Kugel des Gliedes S eine Hohlzylinderfläche des Gliedes Σ, welches mit einem Längsschnitt versehen ist. Die Punkte des Gliedes S können dann, soweit es die Gestaltung der Glieder zuläßt, beliebig im Raum in bezug auf das Glied Σ bewegt werden. Dasselbe gilt von der Bewegung der Punkte des Gliedes Σ gegen das Glied S, und die Beweglichkeit dieser beiden Glieder ist raumläufig. – Bei jeder Bewegung von S gegen Σ beschränkt sich aber die Bewegung des Kugelmittelpunktes M auf die geradlinige Bewegung in der Achse der Zylinderfläche von Σ. Es gibt jedoch keinen Punkt des Gliedes Σ, der sich bei jeder Bewegung von Σ gegen S geradlinig bewegt; dagegen geht aber bei jeder Bewegung von Σ die Achse der Zylinderfläche beständig durch den Kugelmittelpunkt M. Die beiden raumläufigen Bewegungen von S gegen Σ und umgekehrt von Σ gegen S sind demnach nicht als gleichartig zu betrachten. – Wird in Fig. 9 das Glied S mit den drei Spitzen A, B, C auf einer Fläche Φ des Gliedes Σ beliebig bewegt, so ist die Beweglichkeit von S gegen Σ raumläufig und ebenso umgekehrt, wenn Σ mit der Fläche Φ auf den drei Spitzen A, B, C des als fest betrachteten Gliedes S bewegt wird. Bei der Bewegung von S gegen Σ zeichnen sich aber die drei Spitzenpunkte A, B, C dadurch aus, daß ihre Bewegung auf die Fläche Φ beschränkt ist. Nehmen wir nun an, daß bei der Bewegung von S gegen Σ eine Spitze, z.B. A, sich auf der Fläche Φ in einer bestimmten Bahnkurve bewegt, dann ist die Beweglichkeit von S gegen Σ flächenläufig. Bewegen sich ferner zwei Spitzen A, B in bestimmten Bahnen auf der Fläche Φ, dann ist die Beweglichkeit von S kurvenläufig bezw. zwangläufig. Dieselben Beziehungen ergeben sich umgekehrt bei diesen Beschränkungen, wenn S als fest angesehen und Σ gegen S bewegt gedacht wird. – So mannigfaltig, wie die Flächenteile sein können, in denen sich die Glieder während der Bewegung berühren, so mannigfaltig ist auch die Beweglichkeit der Gliederpaare.

Burmester.

Fig. 1.

Fig. 2., Fig. 3., Fig. 5., Fig. 6., Fig. 7.

Fig. 4.

Fig. 8., Fig. 9.