- Kernformel
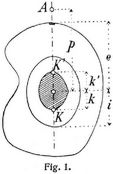
Kernformel. Nach der Lehre von der Biegung (s.d.) ist die größte in einem Balkenquerschnitt auftretende Normalspannung σ = P : F + e M : J, worin P die Normalkraft, M ihr statisches Moment hinsichtlich des Schwerpunktes, F den Flächeninhalt, J das Trägheitsmoment des Querschnittes und e die Entfernung des am stärksten beanspruchten Querschnittselementes von der Schwerlinie bedeutet. Ist A der Angriffspunkt der Kraft P auf einer der Hauptachsen des Querschnitts, so ist (Fig. 1) M = P p. Ferner ist nach der Theorie der Trägheitsellipse (s.d.) J = F i2 und nach der Theorie des Kerns (s.d.) i2 = e · k Daraus folgt
σ = Pi2/J + (e P p)/J = P e (k + p)/J
oder wenn man noch J : e = W = F k setzt:
σ = P (k + p)/F k.
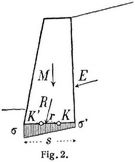
Der Zähler dieses Bruches ist das Moment der Kraft P hinsichtlich des Kernpunktes K; wir nennen es Kernmoment. Der Nenner wird Widerstandsmoment genannt. Die Formel gilt auch für unsymmetrische Querschnitte e, wenn A nicht auf einer Hauptachse liegt. Folglich läßt sich sagen: Die größte im Querschnitt auftretende Normalspannung ist gleich dem Kernmoment der angreifenden Kraft, geteilt durch das Widerstandsmoment des Querschnitts. Vertauscht man den unteren Kernpunkt mit dem oberen, so gelangt man mittels desselben Satzes zur kleinsten Normalspannung. Die Kernformel läßt sich unter anderm mit Vorteil zur Berechnung der Randspannungen in Mauerwerkskörpern verwenden. Ist für eine Stützmauer (Fig. 2) R die Mittelkraft von Erddruck E und Mauergewicht M, so teilt man, um die größte Fundamentspannung zu finden, die Breite s in drei gleiche Teile und mißt den Hebelarm r von R hinsichtlich des Kernpunktes K. Ersetzt man dann F durch s und k durch 1/6 s (vgl. Kern eines Rechteckes), so ergibt sich gemäß obiger Formel die Spannung an der linken Kante σ = 6 R r : s2. Vertauscht man K mit K', so bekommt man die Spannung σ' an der rechten Kante. Eine ausgedehnte und wichtige Anwendung findet die Kernformel bei der Berechnung der Bögen. Da es dabei auf die Ermittlung der Grenzwerte der Randspannungen ankommt und diese proportional den Kernmomenten sind, so berechnet man bei diesen Konstruktionen am besten die Grenzwerte der Randspannungen aus den Einflußlinien für die Kernmomente. Literatur: Ritter, W., Civilingen. 1876, S. 309; Ders., Anwendungen der graphischen Statik, 1. Teil, S. 59, Zürich 1888; Müller-Breslau, Graphische Statik, Bd. 1, Stuttgart 1905.
Mörsch.
http://www.zeno.org/Lueger-1904.