- Kernlinien
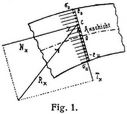
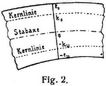
Kernlinien. – Kernpunkte eines Bogenquerschnitts (s. Bogen, Bogenträger, Bd. 2, S. 141) heißen diejenigen oberhalb und unterhalb der Bogenachse in der Bogenebene gelegenen Punkte des Querschnittes, zwischen welchen die resultierende Schnittkraft Rx (Fig. 1) und damit auch ihre Komponenten, die Normalkraft Nx und Transversalkraft Tx, angreifen müssen, wenn alle Normalspannungen o des Querschnitts von gleichem Vorzeichen sein sollen (Druck bei Sprengbogen). Durch Verbindung der oberen bezw. der unteren Kernpunkte aller einzelnen Querschnitte entstehen die beiden Kernlinien des Bogens (Fig. 2).
Bezeichnen F, J Flächeninhalt und Trägheitsmoment eines Querschnitts, eo, eu die absoluten Entfernungen des obersten und untersten Querschnittselements von der Achsschicht und r den Krümmungsradius der Achse beim fraglichen Querschnitt, so hat man die absoluten Entfernungen des oberen und unteren Kernpunktes von der Achse [4], S. 27:
k0 = J/F eu – J/r, ku = J/F eo + J/r
1.
Bei Bogenbrücken sind die r so groß, daß unter Vernachlässigung von J/r gesetzt zu werden pflegen:
k0 = J/F eu, ku = J/F eo.
2.
Für rechteckige Querschnitte (Gewölbe) von der Höhe h und Breite b erhält man mit F = b h, J = b h3/12, eo = eu = h/2 aus 2. ko = ku = h/6. Bei Bogen mit durchbrochenen Wandungen (Fachwerkbogen, Gitterbogen) fallen die Kernlinien annähernd mit den Gurtungsschwerlinien zusammen, bei vollwandigen Bogen liegen sie näher nach der Achse hin. Bezeichnet c = Mx : Nx die Entfernung des Angriffspunktes von Rx oder Nx von der Achse, bei Sprengbogen positiv nach oben, negativ nach unten, dann lassen sich die Normalspannungen im obersten und untersten Querschnittselement, zwischen welchen die Werte aller übrigen Normalspannungen des Querschnitts liegen, ausdrücken:
σo = Nx/F (1 + c/ku), σu = Nx/F (1 – c/ko).
3.
Da die Verbindungslinie der durch die c bestimmten Angriffspunkte von Rx oder Nx Stützlinie heißt, so läßt sich auch aussprechen: Sämtliche Normalspannungen eines Querschnitts haben unter sich und mit ihrer Resultante Nx einerlei Vorzeichen (Druck bei Sprengbogen), wenn bei diesem Querschnitte die Stützlinie zwischen den Kernlinien liegt (bei Gewölben im mittleren Drittel). Andernfalls sind die Vorzeichen der Normalspannungen verschieden und hat für c < – ku die Normalspannung σo, für c > ko die Normalspannung σu das entgegengesetzte Vorzeichen wie Nx. Ueber die Anwendung der Kernlinien bei Bestimmung der ungünstigsten Belastungen s. Bogen, einfache, Bogenfachwerke; vgl. a. Kern.
Literatur: [1] Winkler, Die Lehre von der Elastizität und Festigkeit, Prag 1867, §§ 288, 292–296. – [2] Müller-Breslau, Theorie und Berechnung der eisernen Bogenbrücken I, Berlin 1880, §§ 8, 10, 14. – [3] Krohn, Resultate aus der Theorie des Brückenbaues II, Leipzig 1883, §§ 1, 5, 11, 12, 18, 19. – [4] Weyrauch, Die elastischen Bogenträger, München 1897, 8, 11, auch S. 125, 273 u.s.w. – [5] Mehrtens, Vorlesungen über Statik der Baukonstruktionen und Festigkeitslehre, I, Leipzig 1903, S. 345, 357; II, Leipzig 1904, S. 168. – [6] Handbuch der Ingenieurwissensch., II, 5, Eiserne Bogen- und Hängebrücken, Leipzig 1906, S. 69.
Weyrauch.
http://www.zeno.org/Lueger-1904.