- Blechträger
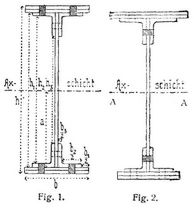
Blechträger heißen eiserne Träger (s.d.), die aus zwei durch Winkeleisen allein oder durch solche und Deckplatten gebildeten Bändern, den Gurtungen (Gurten), und einer diese verbindenden ebenen Blechwand (Siebblech, Vertikalplatte) gebildet sind, so daß Querschnitte von der in Fig. 1 und 2 angedeuteten Form entstehen. Die Querschnitte sind stets symmetrisch zur Mittellinie der Blechwand angeordnet, die damit eine Hauptträgheitsachse bildet (s. Trägheitsmomente ebener Figuren), während die andre, AA, im Schwerpunkt des Querschnitts senkrecht zu ihr lieht und meist ebenfalls eine Symmetrieachse des Querschnitts ist[54] (Fig. 1). Bei Blechbalken (s. Balken) würden nur Rücksichten, die mit der Tragfähigkeit nichts zu tun haben, unsymmetrische Formen rechtfertigen können, und selbst für Blechbogen (s. Bogen) sind im allgemeinen zu AA symmetrische Formen zu empfehlen, deren Höhe nach Bedürfnis veränderlich sein kann. Die Verbindung der vertikalen Blechwand mit den Winkeleisen und dieser mit den Deckplatten (Kopfplatten, Gurtplatten, Horizontalplatten) erfolgt durch Nieten, die so zu verteilen sind, daß die Querschnitte möglichst wenig verschwächt werden (Fig. 3). Die äußeren Kräfte (Lallen, Stützenreaktionen) sollen, soweit erreichbar, in der Mittelebene der Blechwand (Trägerebene, Biegungsebene) angreifen, für Sicherheit gegen seitliche Ausbiegung der letzteren muß besonders gesorgt sein (s. unten III und Blechträgerbrücken).
Die Blechträger bilden den Uebergang von den vollen Balken und Bogen (z.B. rechteckigen Querschnitts) zu den Trägern mit durchbrochener Wand (Gitterträger, Fachwerkträger). Bei ersteren wird das Material in der Nähe der Achsschicht nicht genügend ausgenutzt. Indem man es von da nach den stärker beanspruchten Stellen brachte, wurde bei gleicher Querschnittsfläche F die Tragfähigkeit erhöht, bei gleicher Tragfähigkeit der Materialverbrauch verringert. Zahlenmäßig zeigt sich dies in der Erhöhung der Trägheitsmomente J und Widerstandsmomente W bei bestimmtem F (s. Trägheitsmomente ebener Figuren und Biegung I). Für genügend kleine Spannweiten und Belastungen, wie sie besonders im Hochbau vorkommen, dienen die I-Träger dem gleichen Zwecke. Wo diese nicht ausreichen (die deutschen Normalprofile [22] reichen bis h = 55 cm, b = 20 cm, J = 99054 cm3, W = 3602 ccm), kommen zunächst Blechträger in Frage, die jetzt als einfache Balken in Europa selten über 15 m lang (Ausnahmen s. Balken), als Bogen aber bis zu weit größeren Spannweiten ausgeführt werden. So hat die 1893 dem Verkehr übergebene Straßenbrücke über den Neckar bei Cannstatt [23], S. 259, in jeder Oeffnung sechs parallele Parabelblechbogen mit Kämpfergelenken von Spannweiten bis zu 50,48 m (Pfeile der Achsen und Höhen s. unten); die eingleisige Rohrbachbrücke der Gotthardbahn [5] besitzt zwei vollwandige Kreisbogenträger ohne Gelenke von 60 m Spannweite (Pfeil der Achse gegen die Verbindungsgerade der mit 1,5 m Höhendifferenz angeordneten Auflager 6 m, Höhe in der Mitte 1 m, an den Kämpfern 1,4 m), während die vier Blechbogen von kreisförmiger Achse mit Kämpfergelenken des zweigleisigen Viaduc de l'Erdre [1] sogar 95 m Spannweite aufweisen (Pfeil 12,07 m, Höhe in der Mitte 2,2 m, an den Kämpfern 2,5 m, Dicke des Stehblechs 1,1 cm). Auch die Straßenbrücke über den Harlem-River in New York [9] mit zwei Oeffnungen von 155,235 m Spannweite ist als Blechträgerbrücke anzusehen; die sechs parallelen Kreisbogenträger (Pfeil 27,432 m, Bogenhöhe rund 4 m) bestehen aus je 34 Wölbestücken mit 3,378 m hohem Siebblech von 1 cm Dicke und Gurtungen aus je sechs Winkeleisen und zwei Plattenlagen.
Das Trägheitsmoment von Blechträgerquerschnitten interessiert besonders bezüglich der Schwerpunktsachse AA, die für Balken unter den Voraussetzungen der Biegungstheorie die neutrale Achse ist (s. Biegung I und Achse, neutrale). Da das Trägheitsmoment der Summe oder Differenz zweier Figuren gleich der Summe oder Differenz der Trägheitsmomente der einzelnen Figuren ist, und für ein Rechteck der Seiten b, h in Hinsicht der Seite b und einer dieser parallelen Achse durch den Schwerpunkt die Trägheitsmomente sich ausdrücken:
J = bh3/3, J = bh3/12
so hat man z. B. für den zu AA symmetrischen Querschnitt Fig. 1:
Bei Verschwächung durch n Niete von der Schaftlänge c, Dicke d und mittleren Entfernung von der Achsschicht a hat man rechts n c d a2 zu subtrahieren, doch ist eine Nietverschwächung jedenfalls nur bei Berechnung der Dimensionen und Spannungen, nicht der Formänderungen und davon abhängiger Größen zu berücksichtigen. Für unsymmetrische Querschnitte (Fig. 2) wären die Trägheitsmomente der Teile oberhalb und unterhalb AA auf Grund der erstangeführten Formel für das Rechteck getrennt zu ermitteln und dann zu addieren. Mit dem Trägheitsmoment wird auch das Widerstandsmoment
bekannt, worin e die größte Entfernung eines Querschnittselements von AA, also bei symmetrischen Querschnitten h/2 bedeutet.
Die auf dem angegebenen Wege erhaltenen Ausdrücke des Trägheitsmoments sind nicht für alle Zwecke bequem, weshalb man verschiedene Näherungsformeln abgeleitet hat, so für den symmetrischen Querschnitt:
und für den unsymmetrischen Querschnitt:
oder noch etwas weniger genau:
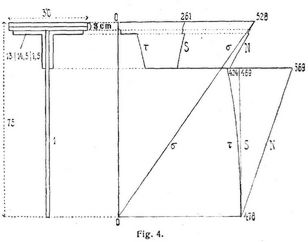
[55] Hierin sind h, ho, hu die Entfernungen des oberen und unteren Gurtungsschwerpunktes von einander und von AA. Für den in Fig. 4 zur Hälfte angedeuteten Querschnitt lieferte 3. gegenüber dem aus 1. folgenden J = 1937 945 cm4 einen um 0,97% zu kleinen, mit δ = 0 (Vernachlässigung des Widerstands der Vertikalplatte) aber einen um 13,16% zu kleinen Wert. Für einen unsymmetrischen Querschnitt, Stehblech 40/1 cm, vier Winkeleisen von 8,8/1 cm, eine Horizontalplatte nur für eine Gurtung 20/1 cm, ergaben gegenüber dem genauen Werte J = 31350 cm4 die Gleichungen 4. und 5. um 6,2 und 9,5% zu kleine, mit δ = 0 jedoch um 20,0 und 26,6% zu kleine, d.h. zu ungünstige Werte. Mehrfach hat man die J, W für gangbare Dimensionen von Blechträgern in Tabellen zusammengestellt [6], [11], [17], [18], [22], [26], [27] u.s.w.
I. Blechbalken.
Diese pflegen für l m Spannweite eine Höhe von 1/8 l bis 1/12 l m Winkeleisen von mindestens 6 + 0,2 l cm Schenkellänge und nach Bedürfnis 1–3 Deckplatten von mindestens 15 + 0,5 l cm Breite zu erhalten. Gurtungen im allgemeinen parallel, nur in einzelnen Fällen hat man dem Untergurt aus ästhetischen Gründen Bogenform gegeben (durchlaufende Balken der Limmatbrücke in Zürich, Müllerstraßenunterführung in Berlin u s. w.). Die Stärke der Vertikalplatte wird von vornherein 0,9–1,2 cm angenommen; unter 0,9 zu gehen, ist mit Rücksicht auf Rost und seitliche Einwirkungen nicht zu empfehlen. Zum Widerstande gegen vertikale und horizontale Schubkräfte würde bei τ = 4/5 s zulässiger Schubbeanspruchung pro Flächeneinheit genügen:
(vgl. Biegung, zweite Formel 2, 5 zulässige Beanspruchung auf Zug, S0 Wert von Sv für v = 0). Unter Mitberücksichtigung der schiefen Wandspannungen (s. Biegung, Formeln 3) ließe sich für einfache und durchlaufende Träger etwa setzen [10], S. 125:
unter Vx, wie oben, die größte Vertikalkraft im betreffenden Querschnitt x (s. Balken, auch einfache und durchlaufende), unter h die Entfernung der Gurtungsschwerpunkte verstanden, doch liefern diese Formeln meist zu geringe Stärken.
Die Querschnittsfeststellung erfolgt in der Praxis allgemein auf Grund der größten vorkommenden Normalspannungen der Querschnitte, wobei nicht ausgeschlossen ist, daß die größten schiefen Spannungen und selbst die reduzierten Hauptspannungen (s. Festigkeitsbedingung) nachträglich berechnet werden. Ist bei einem Querschnitte x Mx das größte Angriffsmoment (s. Balken, einfache und durchlaufende), e die Entfernung der äußersten Faser von der Achsschicht, so hat man das nötige Trägheitsmoment J und Widerstandsmoment W:
worin s die größte zulässige Normalspannung(s. Biegungsfestigkeit). Soll der Träger konstanten Querschnitt erhalten, so ist dieser dem größten überhaupt vorkommenden Moment anzupassen (absolutes Maximalmoment, vgl. Balken, einfache). – Die Feststellung des Trägerquerschnitts nach 8. bietet dann keine Schwierigkeit, wenn die J, e oder W für geeignete Abmessungen in Tabellen zusammengestellt sind. In andern Fällen ergibt sich der nötige nutzbare Gurtungsquerschnitt für den gewöhnlichen Fall symmetrischer Anordnung am einfachsten aus 3., 8., mit e = h/2:
Findet bei x ein Stoß der Vertikalplatte statt, so ist im zweiten Gliede statt h nur die nutzbare Höhe einzusetzen, die mit 3/4 h nicht leicht zu hoch gerechnet wird. Selbstverständlich wird man Stöße der Vertikalplatte am liebsten dahin verlegen, wo der Querschnitt ohnehin größer als nötig ist. Mitunter werden die Höhe h0 und das Widerstandsmoment W0 des Trägers ohne Deckplatten von vornherein gewählt und dann durch Zugabe einer genügenden Anzahl n von Deckplatten der Dicke d und des nutzbaren Querschnitts p in jeder Gurtung das nötige Widerstandsmoment W hergestellt. Die fragliche Anzahl n ist dann bestimmt durch:
[8], S. 168. Man kann rechts für 2 n d zunächst Null oder einen geschätzten Wert setzen und hierauf mit dem ermittelten n d nochmals rechnen oder kontrollieren. Ist der Querschnitt mit Hilfe von 9. oder auf sonstige Weise ermittelt, so kann man J oder W nach 1., 2. berechnen und feststellen, ob 8. genügt wird. Auf Zusatzkräfte, die von der (vertikalen) Belastung unabhängig sind (Winddruck u.s.w.), ist selbstverständlich Rücksicht zunehmen, auch Nebenspannungen (s.d.) sind mitunter zu beachten; s. z.B. [19].
Bei durchlaufenden Trägern können die schiefen Wandspannungen N bei den Zwischenstützen (wo Mx und Vx gleichzeitig groß werden) erheblich größer werden als die horizontalen [56] Normalspannungen σ und die horizontalen und vertikalen Schubspannungen τ. In Fig. 4 sind die σ, τ, N, S für einen solchen Fall in den zugehörigen Entfernungen von der Achsschicht als horizontale Ordinaten aufgetragen (s. Biegung, Formeln 2 und 3), wobei Mx= 135 m t, Vx = 64 t war. Während das größte σ im Querschnitt (wie am ganzen Träger) nur 528 kg pro Quadratzentimeter betrug, erreichte N den Wert 669 kg. Man tut also gut, wenigstens bei den Zwischenstützen durchlaufender Blechträger nachträglich zu kontrollieren, ob die größten N am Gurtungsbeginn nicht über das zulässige Maß hinausgehen.
Bei Bestimmung der Nietteilung t (Fig. 3) pflegen Schubspannungen von 4/5 s im Querschnitt und 2 s Druck pro Flächeneinheit Projektion der Lochlaibung zugelassen zu werden. Die Entfernung der Niete zum Anschlusse der Winkeleisen an die Blechwand darf dann bei x höchstens betragen [10], S. 150:
worin d den Nietdurchmesser bezeichnet. Die Niete zur Befestigung der Deckplatten erhalten meist ohne Berechnung in jeder Reihe die gleiche Entfernung t (Fig. 3), obgleich die Teilung im allgemeinen weiter sein könnte [10], § 42. Da Vx bei einfachen wie bei durchlaufenden Trägern an den Auflagern am größten wird, so ergibt sich t daselbst am kleinsten. Nach der Mitte hin kann streckenweise eine weitere Teilung gewählt werden, sofern nicht praktische Gründe (Einfachheit, Dichtheit der Fuge u.s.w.) dagegen sprechen. Zum Stoße der Vertikalplatte genügen bei den stets angewendeten doppelten Laschen
Niete auf jeder Seite der Stoßfuge, wenn d den Nietdurchmesser und hn die nutzbare Höhe der Vertikalplatte (in der äußersten Nietreihe nach dem Stoße hin) bedeuten. Näheres s. [10], § 45.
II. Blechbogen.
Bei diesen lassen sich die Querschnitte den wirkenden Kräften noch weniger genau als bei Balken anpassen, weil für symmetrisch zur Achsschicht angeordnete Querschnitte die Normalspannungen in der obersten und untersten Faser im allgemeinen nicht gleich werden, auch die Veränderlichkeit ihrer Grenzwerte von der Mitte nach den Auflagern hin keine einfache ist. Wollte man aber die Querschnitte den Beanspruchungen entsprechend unsymmetrisch herstellen, so würde die Stabachse nicht mehr die vorausgesetzte regelmäßige Form erhalten und die Konstruktion an Einfachheit verlieren, ohne daß die Einhaltung der betreffenden Beanspruchungen gesichert erschiene. Durch geeignete Wahl der Trägerhöhe und Gurtungsquerschnitte läßt sich übrigens stets erreichen, daß auch bei symmetrischen Querschnitten keine übermäßige Verschiedenheit in der Ausnutzung des Materials eintritt. Für die Blechbogen mit zwei Gelenken der obenerwähnten neuen Neckarbrücke bei Cannstatt betragen Spannweite und Pfeil der Achse in den Oeffnungen:
I II III IV V l = 45,51 48 50,48 48 45,51 m, f = 4,375 4,735 4,855 4,505 3,695 m. Die Fahrbahn wird durch sechs parallele Bogen aus Martinflußeisen getragen, bestehend aus je vier Winkeleisen von 9/9/1,2 cm, zwei durchgehenden Horizontalplatten von 38/1,4 cm, zwei horizontalen Verstärkungsplatten von 38/1,2 cm, die über den Scheitel weggehend etwa 4 m von den Auflagern endigen, und einer Vertikalplatte von δ = 1,2 cm Dicke, deren Höhe vom Scheitel nach den Auflagern so zunimmt, daß
min h = 75 79 83 79 75 cm, max h = 86 90 94 90 86 cm. Die größten Normalspannungen im Obergurt und Untergurt, einschließlich des Einflusses der Temperaturänderungen ergaben sich z.B. in Oeffnung IV in Entfernungen x von den Auflagern wie folgt [23] S. 281:
Bei Mitwirkung der Straßenwalze wurden die Grenzwerte in der Nähe der Mitte etwas höher, in der Mitte selbst σo = 901, σu = 900 kg [23] S. 283. Zu dieser Annäherung hat ein künstlicher Horizontalschub (s. Horizontalschub) von 1950 kg insoweit beigetragen, als dadurch die σo um – 13 bis – 70, die σu um 26 bis 81 kg qcm geändert wurden. Für Eigengewicht allein, dem die längste Zeit annähernd bestehenden Belastungsfall, wurde fast vollständige Gleichheit der σo, σu erreicht.
Bezeichnen beim Querschnitte x Mx, Nx das Angriffsmoment und die Normalkraft (s. Bogen, auch einfache und durchlaufende), eo, eu die Entfernungen des höchsten und tiefsten Querschnittselements von der Achsschicht, dann sind die Normalspannungen in diesen Entfernungen genügend genau (s. Biegung II):
und für symmetrisch zur Achsschicht angeordnete Querschnitte vom Widerstandsmoment W:
Für die ganzen Gurtungsbeanspruchungen können als Näherungswerte Verwendung finden:
[57] worin o, u die mittleren Beanspruchungen des Obergurts und Untergurts pro Flächeneinheit ihrer Querschnitte fo, fu und h die Entfernung der Gurtungsschwerpunkte bedeuten. Für symmetrisch zur Achsschicht angeordnete Querschnitte x werden mit fo = fu = f:
Auf Grund vorstehender Gleichungen kann die Ermittlung der Querschnitte zunächst in vorläufiger Weise, wie sogleich anzugeben, erfolgen. Auf etwaige Festsetzungen bezüglich der Trägerhöhe (Zunahme nach den Enden u.s.w.) ist dabei Rücksicht zu nehmen, die Dicke der Vertikalplatte wird von vornherein gewählt (meist 1–1,2 cm). Die Winkeleisen erhalten wenn möglich innerhalb einer Oeffnung konstanten Querschnitt, so daß die Aenderungen der Gurtungsquerschnitte nur durch Zugeben oder Weglassen von Horizontalplatten stattfinden. Temperatureinflüsse brauchen bei der vorläufigen Berechnung nicht berücksichtigt zu werden.
Einfachstes Verfahren. Beispiel [23], S. 260. Man bestimmt für eine genügende Anzahl Querschnitte unter Verwendung einfachster Formeln für statisch unbestimmte Größen (H bei Bogen mit zwei Gelenken, H, M, M' bei Bogen ohne Gelenke, s. Bogen), Mx, Nx bei Belastung durch Eigengewicht allein, bei Vollbelastung des ganzen Trägers und bei einseitiger Belastung bis zur Trägermitte, womit für jeden Querschnitt 4 Werte von Mx, Nx bekannt werden (Symmetrie berücksichtigt), unter denen sich die für die schätzungsweisen Grenzwerte von σo, σu oder o, u maßgebenden befinden. Indem man nun zusammengehörige Mx, Nx am bequemsten in 16., 15., etwas genauer in 14., 13. verwendet, und für σ oder s einen etwas unter dem zulässigen Grenzdruck pro Flächeneinheit bleibenden Wert einführt, läßt sich der vorläufige Bogenquerschnitt durch einiges Probieren ermitteln. Bei der obenerwähnten Neckarbrücke war der zulässige Grenzdruck pro Quadratzentimeter 1000 kg, während für Beanspruchungen durch Belastungen 800 (1 + min σ/2 max σ) zugelassen war, sofern nicht unter Hinzurechnung der Temperatureinflüsse jener Grenzdruck von 1000 kg überschritten wurde. Für die vorläufige Berechnung würde hier etwa 750 kg pro Quadratzentimeter anzunehmen gewesen sein, bei drei Gelenken etwas mehr, ohne Gelenke etwas weniger.
Zweites Verfahren. Man bestimmt für eine genügende Anzahl Querschnitte unter Verwendung einfachster Formeln für statisch unbestimmte Größen die Mx, Nx bei denjenigen Belastungen, welche die Grenzwerte von Mx ergeben, wobei die Bogenachse an Stelle der Kernlinien Verwendung findet (s. am Schlusse von Bogen, einfache oder [23], S. 40). Mit den so erhaltenen Werkpaaren liefern 13.–16. die ersten Annäherungen der Grenzwerte von σo, σu bezw. von o, u. Indem man für die größten derselben einen Wert etwas unter dem zulässigen Grenzdruck setzt (wobei man des genaueren Vorgehens wegen eher etwas höher als oben gehen kann), läßt sich der vorläufige Querschnitt durch einiges Probieren ermitteln. – Andre Verfahren zur vorläufigen Ermittlung der Querschnitte s. bei Krohn [2], II, S. 43, 118; Müller-Breslau [3], S. 60, 165, 181; Melan [7], IV, S. 101.
Nachdem die vorläufige Ermittlung der Querschnitte beendigt ist, wird eine Revision, Ausgleichung und Berichtigung der Bogen mit Rücksicht auf ästhetische und konstruktive Bedürfnisse vorgenommen (für die Bogenhöhe graphisch). Alsdann erfolgt die endgültige Berechnung, wobei sämtliche Querschnitte bekannt sind, so daß die genaueren Formeln Verwendung finden können (s. Biegung II, Bogen, einfache und durchlaufende). Es handelt sich auch hier in erster Linie um die Grenzwerte der σo, σu bei Zusammenwirken von Belastung, Temperaturänderungen u.s.w., wobei stets nach 13., 14. gerechnet werden kann, da die Verwendung umständlicherer Formeln keine wesentlich genaueren Resultate liefert. Bei der obenerwähnten Berechnung der Cannstatter Brücke hätten sich mittels der genaueren Formel 22. unter Biegung II für die Maximalwerte σo, σu Abweichungen von 0 bis etwa 0,27% ergeben. Festzustellen ist auch, daß genügende Sicherheit gegen seitliches Einknicken durch die Axialkraft Nx besteht (s. Knickfestigkeit und [23], S. 284). Sollten sich bei der genaueren Berechnung einzelne Aenderungen als wünschenswert erweisen (Dicke, Breite, Länge von Horizontalplatten), so können diese meist vorgenommen werden, ohne daß die Berechnung wiederholt zu werden braucht, da der Einfluß auf die Mx, Nx gering und vielfach kaum merklich ist, so daß es genügt, die betreffenden σ nach 13., 14. entsprechend den neuen F und J oder W zu korrigieren.
Man kann noch feststellen wollen, ob die angenommene Stärke der Vertikalplatte gegenüber den Kräften in der Wandebene genügt. Für die Quer- und Längsschubspannungen würde entsprechend 6. ausreichen:
unter Tx die größte Transversalkraft bei x verstanden (s. Bogen, auch einfache und durchlaufende). Analog 7. kann man statt dessen verlangen:
doch wird auch diese Formel wohl immer kleinere Werte als die gewählten liefern, da die Tx bei Bogen weit geringer als bei Balken ausfallen. Die größte zulässige Nietteilung zur Verbindung des Stehblechs mit den Winkeleisen wäre entsprechend 11.:
doch pflegt diese Formel zu große t zu liefern, da man nicht leicht über 6 d–8 d hinausgehen wird. Die Nietteilung zum Anschlusse der Deckplatten pflegt derjenigen im Stehblech zu entsprechen (Fig. 3). Für die Nietzahl zum Stoße der letzteren kann Formel 12 beibehalten werden.
[58] III. Versuche mit Blechbalken.
Ueber die Widerstandsfähigkeit von Blechbalken sind in neuerer Zeit mehrfach Versuche angestellt worden, woraus sich u.a. auf das Verhältnis β der Biegungsfestigkeit b (s.d.) des fertigen Trägers zur absoluten Zugfestigkeit z des Gurtmaterials schließen ließ. Bekannt geworden sind besonders die Versuche mit 32 Trägern von 5,8 m Spannweite (Siebblech 68,5/0,7 cm, Winkeleisen 7/7/0,7 cm, einfache Deckplatten 150,7 cm) aus Schweißeisen und Bessemermetall, die 1876 auf Veranlassung der holländischen Regierung in der Harkortschen Brückenbauanstalt ausgeführt wurden [4], [12], S. 220. Sie lieferten im Mittel für Schweißeisen von z = 3900 kg qcm Zugfestigkeit β = 0,94, dagegen für Bessemermetall von z = 4600, 6600, 8400 kg bezw. β = 0,77, – 0,59, – 0,74, was die Anwendung des Flußeisens im Brückenbau verzögerte. – Tetmajer erhielt bei Versuchen mit je acht Blechbalken von 3,6 bis 6,6 m Spannweite (Siebblech 40 bis 70/0,9 cm, Winkeleisen 9/9/0,9 cm, einfache Deckplatten 22 0,9 cm) aus Schweißeisen und basigem Konvertereisen für das Schweißeisen von z = 3750 kg ebenfalls im Mittel 11 = 0,94, für das Flußeisen von z – 4510 kg jedoch ß = 0,85 [12], S. 225. – Eine Kommission des österreichischen Ingenieur- und Architektenvereins fand bei Versuchen mit zwei verbundenen Trägern von 10 m Spannweite (Stahlblech 801 cm, Winkeleisen 7/7 0,8 cm, gegen die Mitte eine und zwei Deckplatten von 160,8 cm) aus Martinflußeisen von z = 3990 kg den Beginn von Knickerscheinungen in den Druckgurten bei β = 0,77. Nach weiterer Belastung trat vollständige Deformation der Druckgurten, jedoch ohne Spur von Rissen, ein [15], S. 70, 72, 99. Es wird empfohlen, im Gegensatze zu den Versuchsträgern, behufs möglichster Versteifung der Druckgurten die Deckplatten derselben stets bis zur nächsten Vertikalsteife, wo der Horizontalverband anschließt, fortzuführen. – Anläßlich des Baues der neuen Eisenbahnbrücken bei Dirschau und Marienburg wurden Versuche mit sechs Blechträgern aus Thomaseisen von 3 m Spannweite ausgeführt (Siebblech 40/1 cm, Winkeleisen 8/81,2 cm, einfache Deckplatten 20/1 cm, [13], S. 718). Die Biegungsfestigkeit ergab sich durchschnittlich nahezu gleich der Zugfestigkeit. Zwei Träger mit gestanzten Nietlöchern brachen auf der Zugseite, während die vier Träger mit gebohrten Löchern ihre Tragfähigkeit durch Verwinden verloren. Erstere zeigten geringere Fertigkeit als letztere Zwei gewalzte I-Träger von annähernd gleichem Trägheitsmoment (Widerstandsmoment?) wie die Blechbalken ließen nicht die gleiche Belastung wie die letzteren zu, weil sie sich der mangelnden Querversteifung wegen stark seitlich ausbogen. – Die Gutehoffnungshütte stellte in Gemeinschaft mit den Eisenbahndirektionen Köln (linksrheinisch) und Elberfeld Versuche an. Von je zwei Blechträgern der Spannweite 3 m (Siebblech 36,51 cm, Winkeleisen 881,2 cm, einfache Deckplatten 20/1 cm [14], S. 808), aus Schweißeisen, weichem und hartem Martineisen wurde einer schlecht gearbeitet (Kanten mit der Schere geschnitten; Nietlöcher gestanzt, gegeneinander versetzt und mit dem Dorn aufgetrieben, Nietung von Hand), der andre gut gearbeitet (Nietlöcher gebohrt und aufgerieben, Nietung durch hydraulischen Druck). Es ergaben sich folgende Werte:
Diese Versuche bestätigen, daß hartes Flußeisen sich nicht für Brückenkonstruktionen eignet, es werden denn auch gewöhnlich Fertigkeiten von 3600–4400 kg pro Quadratzentimeter vorgeschrieben. – Ein bei der Entgleisung eines Schnellzugs durch Verbiegung unbrauchbar gewordener Hauptträger der Neissebrücke bei Loewen von 11,91 m Spannweite (Siebblech 10,181 cm, Winkeleisen 7,8,7,8 1,3 cm, einfache Deckplatten 232,6 cm), der 38 Jahre gedient hatte, sollte in der Mitte bis zum Bruche belastet werden [20]. Bei 2770 kg pro Quadratzentimeter rechnungsmäßiger Normalspannung knickten das Siebblech und der Druckgurt ein, ohne daß sich Risse oder lockere Nieten zeigten. Nimmt man die nicht bestimmte Zugfestigkeit des Materials zu z = 3500 kg qcm an, so hat der Träger noch bis β = 0,79 widerstanden. Es war jedoch anzunehmen, daß er im ganzen Ueberbau eine weit höhere Beanspruchung ausgehalten hätte, weil dann das Siebblech und der Druckgurt durch die Querverbindungen besser gegen Knicken gesichert gewesen wären.
Auch mit andern vollwandigen eisernen Balkenträgern wurden Bruchversuche angestellt; so in Wien [21] mit einem Schweißeisenbalken von 7,5 m Spannweite und Kastenquerschnitt aus zwei Stehblechen von 50,41 cm, Kopf- und Fußdeckplatten von 34/1,3 cm, zwei Winkeleisen von 8/81 cm im Druckgurt und vier ebensolchen im Zuggurt. Der Träger von 8,3 m Länge war aus einem Hauptträger von 11,2 m Spannweite und 12,95 m Länge hergerichtet worden, der mit seinem Zwillingsbruder von 1858 bis 1888 der Brücke über den Kundlerbach der Eisenbahn Innsbruck-Kufstein gedient und dabei rechnungsmäßige Beanspruchungen bis 1250 kg qcm auf Zug und bis 1370 kg qcm auf Druck ausgehalten hatte. Nachdem die elastischen Einsenkungen bis zur Erschöpfung der Widerstandsfähigkeit proportional der Belastung geblieben waren (wozu aber erhebliche bleibende Einsenkungen kamen), trat bei rechnungsmäßigen Normalspannungen von 2603 kg im Zuggurt und 2850 kg im Druckgurt Knicken beider Stehbleche ohne Spuren sonstiger Trennungen ein. Da die Zugfertigkeit von Stäben aus den wenigst angestrengt gewesenen Teilen des Trägers zu z = 2827 kg für die Stehbleche und z = 3210 kg für die Deckplatten ermittelt wurde (bei E = 2120000 und 2270000 kg pro Quadratzentimeter Elastizitätsmodul), so wäre in bezug auf das Material der Stehbleche β = 0,92, in bezug auf dasjenige der Deckplatten β = 0,81 gewesen.
Abgesehen vom Material haben sich diejenigen Blechbalken am bellen bewährt, die genügende Stärke der Vertikalplatte und genügende Quersteifigkeit besaßen. Die Nietverschwächung[59] war bei Berechnung der angeführten Versuchsergebnisse, soweit ersichtlich, für beide Gurtungen in Abzug gebracht.
Literatur: [1] Dupuy, Notice sur le viaduc de l'Erdre, Annales des ponts et chaussées 1879, I p. 331. – [2] Krohn, Resultate aus der Theorie des Brückenbaues und deren Anwendung, erläutert durch Beispiele, Aachen, I. Balkenbrücken, 1879, S. 6, 70, 223, II. Bogenbrücken, 1883, S. 1, 43, 118 – [3] Müller-Breslau, Theorie und Berechnung der eisernen Bogenbrücken, I. Die stabförmigen elastischen Bogen, Berlin 1880. – [4] Wochenschrift des Vereines deutscher Ingenieure 1882, S. 5; 1883, S. 84. – [5] Steiner, Zum gegenwärtigen Stand des Brückenbaues, Zeitschr. d. österr. Ing.- und Arch.-Vereins 1883, S. 18. – [6] Zimmermann, Trägheitsmomente, Widerstandsmomente und Gewichte genieteter Blechträger, Berlin 1885. – [7] Handbuch der Ingenieurwissenschaften, Bd. 2, 2. Aufl. Leipzig 1886–1890; II. Balken, von Steiner, 3. Aufl., 1901; III. Bewegliche Brücken, von Fränkel; IV. Bogen, von Melan. Daselbst auch umfallende Literaturangaben. – [8] Müller-Breslau, Die graphische Statik der Baukonstruktionen I, Leipzig 1887. – [9] The Manhattan Bridge over the Harlem River, New York, Engineering 1888, I, p. 425 (Zeitschr. des Ver. deutsch. Ingenieure 1889, S. 1120). – [10] Weyrauch, Die Festigkeitseigenschaften und Methoden der Dimensionenberechnung u.s.w., Leipzig 1889, S.23, 123, 149, 161. – [11] Scharowsky, Widerstandsmomente und Gewichte genieteter Träger, Leipzig 1890. – [12] Tetmajer, Mitteilungen der Anstalt zur Prüfung von Baumaterialien u.s.w., 4. Heft, Zürich 1890, S. 82, 207, 220. – [13] Mehrtens, Ueber die beim Baue der neuen Eisenbahnbrücken in Dirschau und Marienburg mit der Verwendung von Flußeisen gemachten Erfahrungen, Stahl und Eisen 1891, S. 707. – [14] Krohn, Verwendung des Flußeisens im Brückenbau, Stahl und Eisen 1891, S. 804. – [15] Bischoff, Bericht des Brückenmaterialkomitees über die Verwendung des Flußeisens, und Brik, Fachwissenschaftliche Erörterungen hierzu, Zeitschr. des österr. Ing.- und Arch.-Vereins 1891, S. 63, 73. – [16] Huléwicz, Calculs de résistance des ponts et viaducs métalliques à poutres droites, d'après le circulaire ministerielle du 29 août 1891, Paris 1894. – [17] Geusen und Miliczek, »Profile«, Sammlung von Tabellen zum Gebrauche bei der Querschnittsbestimmung eiserner Tragkonstruktionen, Nürnberg 1894/95. – [18] Böhm und John, Widerstandsmomente, Trägheitsmomente und Gewichte von Blechträgern, Berlin 1895. – [19] Häseler, Berechnung eines I-förmigen Trägers auf Verdrehung und Biegung, Zentralblatt der Bauverwaltung 1895, S. 233. – [20] Simon, Bruchbelastung eines Brückenblechträgers, Zentralblatt der Bauverwaltung 1895, S. 250. – [21] Brik, Die Ergebnisse der Belastungsversuche mit einem der Bahnstrecke entnommenen alten Eisenbrückenträger, Zeitschr. d. österr. Ing.- und Arch.-Vereins 1896, S. 97, 109. – [22] Heinzerling und Intze, Deutsches Normalprofilbuch für Walzeisen zu Bau- und Schiffsbauzwecken, Aachen 1897. – [23] Weyrauch, Die elastischen Bogenträger, ihre Theorie und Berechnung entsprechend den Bedürfnissen der Praxis, München 1897. – [24] Häseler, Der Brückenbau, 1. Teil: Die eisernen Brücken, 3. Lief., Braunschweig 1897 (Zwischenträger); 4. Lief., Braunschweig 1900 (Hauptträger). – [25] Fyson, Formulae for the weights and economic depths of plate girders, Engineering 1902, I, p. 338, 463. – [26] Leu, Ausführliche Tabellen für Eisen und Holz zu Decken, Trägern, Stützen und Dächern. Querschnitte, Gewichte, Trägheits- und Widerstandsmomente. Köln 1904. – [27] Tetmajer, Die angewandte Elastizitäts- und Festigkeitslehre, Leipzig und Wien 1904 (Oesterreichische Normalprofile, S. 144).
Weyrauch.
http://www.zeno.org/Lueger-1904.