Konen

Konen, zwei konusförmige Rotationskörper, insbesondere Rotationskegel, die sich um ihre parallel gelagerten Achsen drehen und bei denen die Drehung von einem Rotationskörper auf den andern durch einen Riemen übertragen wird. Sie haben den Zweck, vermittelst seitlicher Verschiebung des Riemens durch eine gleichförmige Drehung eine gesetzmäßig veränderliche Drehung zu bewirken, und werden bei Spinnmaschinen, Zentrifugen und andern Maschinen angewendet [1].

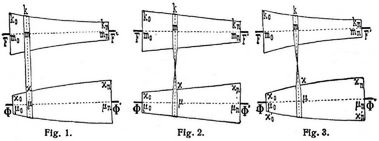
In Fig. 1 sind z.B. die beiden Konen ΦΦ', FF' abgestumpfte Rotationskegel. Nehmen wir an, der Konus ΦΦ' drehe sich gleichförmig, so wird durch Hin- und Herführung des Riemens, der in diesem betrachteten Fall gekreuzt ist, eine veränderliche entgegengesetzte Drehgeschwindigkeit des Konus FF' hervorgebracht; dabei muß aber im allgemeinen eine an den Riemen andrückende Spannrolle (s.d.) angebracht werden, um das Schlaffwerden des Riemens zu vermeiden. Bezeichnen g = μx, r = mk die Radien an der Stelle der Riemenmitte, so stehen die Drehgeschwindigkeiten der Konen ΦΦ', FF' in dem Verhältnis r : g. Soll zur Vereinfachung die Spannrolle beseitigt werden, dann müssen die Konen derart voneinander abhängig gestaltet sein, daß die Straffheit des Riemens während seiner seitlichen Verschiebung erhalten bleibt. Bei gekreuztem Riemen bleibt die Länge desselben konstant, wenn die Summe jener Radien r = g konstant ist [2]. Es müssen demnach die beiden Rotationskegel kongruent, also die Radien μ₀x₀ = m_n k_n, μ_nx_n = m₀ k₀ sein. In dieser einfachsten Gestaltung werden die Konen am meisten ausgeführt und angewendet; aber es ist bei Rotationskegeln die Veränderung der durch gleichförmige Drehung des einen Konus auf den andern übertragenen Drehgeschwindigkeit nicht proportional der seitlichen Verschiebung des Riemens. Wenn diese Proportionalität gefordert wird, dann ergibt sich durch eine einfache Konstruktion, daß in Fig. 2 die beiden Meridiankurven der Konen kongruente gleichseitige Hyperbeln sind [3]. Es ist das Hyperbelstück x'₀ x'_n kongruent k₀ k_n und ferner ist μ₀x'₀ = m_n k_n, μ_n x'_n = m₀ k₀ gemacht. Ist der Riemen nicht gekreuzt, also offen, dann drehen sich die Konen in gleichem Sinne. In diesem Falle ist bei konstanter Riemenlänge die Beziehung jener beiden Radien g, r sehr kompliziert; und es können in Fig. 3 die entsprechenden Meridiankurven x₀ x_n, k₀ k_n nur vermittelst einer Hilfskurve konstruiert werden [3]. In Fig. 3 sind diese entsprechenden Meridiankurven so gestaltet, daß die Veränderung der durch gleichförmige Drehung des einen Konus auf den andern übertragenen Drehgeschwindigkeit der seitlichen Verschiebung der Riemen proportional ist.

Literatur: [1] Th. R. Williams Specification Nr. 5412 vom 19. Sept. 1826 hat die Konen zuerst angewendet, vgl. a. Polytechnisches Journal 1828, Bd. 27, S. 99. – [2] Redtenbacher, Bewegungsmechanismen, Mannheim 1857, S. 8, und dessen Maschinenbau, Mannheim 1862, Bd. 1, S. 349. – [3] Burmester, Lehrbuch der Kinematik, Leipzig 1888, Bd. 1, S. 395–404, enthält eine vollständige Theorie der Konen und die Konstruktionen derselben.

Burmester.

Fig. 1., Fig. 2., Fig. 3.