Massennivellement

Massennivellement, ein von Bruckner erfundenes, von Culmann, Bauernfeind, Eikemeyer, Launhardt und Goering ausgebildetes Verfahren zur graphischen Darstellung der Massenverteilung (s.d.) bei größeren Erdarbeiten.

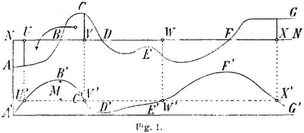
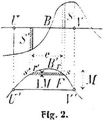
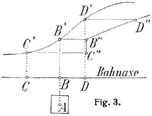
In der Fig. 1 stelle die Linie A B C D E F G das Längenprofil (s.d.) einer projektierten Bahnanlage dar. N N bezeichne die Höhe der Bahnachse (Nivellette). A B und D F sind Dämme oder Aufträge, B D und F G Einschnitte oder Abträge. Teilt man die Bahnlinie in üblicher Weise in Strecken (Stationen) von 50 oder 100 m ein, berechnet für jede Strecke die zu bewegende Erdmasse (s. Erdmassenberechnung, Bd. 3, S. 497), summiert diese Massen fortlaufend und trägt die Summen von einer wagerechten Linie A' G' aus in beliebigem Maßstabe als Ordinaten auf, so gelangt man zu einer zweiten Kurve A' B' C' ..., die man Massenprofil nennt. Auftragmassen rechnet man positiv, Abtragmassen negativ. In Fig. 1 stellt somit die Ordinate von B' die Erdmasse von A bis B, die Ordinate von C' die Erdmasse von A bis C dar, wobei die Masse von B bis C negativ gerechnet, d.h. von der Masse A bis B abgezogen ist Der Umstand, daß das Volumen der Erde beim Graben und Wiederaufschütten zunimmt, wird dadurch berücksichtigt, daß man alle Auftragmassen durch 1 + α dividiert, wo α den Auflockerungsfaktor bedeutet. Aus naheliegenden Gründen besitzt das Massenprofil folgende Eigenschaften: Das Massenprofil steigt im Auftrag und fällt im Abtrag. Je größer der Flächeninhalt des Querprofils, desto steiler das Massenprofil. Nullpunkte des Längenprofils, d.h. Uebergangsstellen von Auftrag in Abtrag oder umgekehrt, ergeben Maximal- oder Minimalpunkte des Massenprofils (Punkte B, D, F). Maximal- und Minimalpunkte des Längenprofils ergeben Wendepunkte des Massenprofils (Punkte C, E u.s.w.). Jede durch das Massenprofil gelegte wagerechte Linie teilt dasselbe in eine Anzahl von »Bergen« und »Tälern«, innerhalb derer die Massen sich ausgleichen. Zieht man beispielsweise die Linie U' V' (»Ausgleichungslinie«) und lotet deren Endpunkte hinauf, so ist die Masse von U bis B gleich der Masse von B bis V und zwar gleich der Höhe M des Berges U' B' V'. Auf dieselbe Weise werden die »Transportstrecken« V W, W X u.s.w. gefunden. In Bergstrecken wird die Erde rückwärts, in Talstrecken vorwärts transportiert. Auch die Transportkosten lassen, sich der[322] Zeichnung entnehmen: In Fig. 2 werde durch zwei benachbarte Querschnitte die Scheibe S herausgeschnitten. Ihr Körperinhalt ergibt sich durch Herunterloten gleich der Ordinatendifferenz von r und s, d.h. gleich Δ M. Zwei wagerechte Linien durch r und s führen zu r' und s' und zur Scheibe S', die den nämlichen Inhalt hat wie S. Man kann sich denken, die Masse S werde nach S' transportiert. Bezeichnet e die Transportweite, so ist Δ M · e die Transportarbeit, sie wird durch den Flächenstreifen r s s' r' dargestellt. Denkt man sich nun die ganze Masse in solche Scheiben zerlegt, so ergibt sich, daß der Flächeninhalt F des Berges U' B' V' die Transportarbeit der Abteilung U V darstellt. Die Transportarten sind daher K = c₁ M + c₂ F, worin c₁ und c₂ zwei hauptsächlich vom Transportmittel abhängige Festwerte bezeichnen (vgl. Bodenbeförderung und Massenverteilung). Die mittlere Transportweite wird gefunden, wenn man F durch M teilt. Zieht man durch ein längeres Massenprofil eine Ausgleichungslinie, so hat man, um die Kosten zu finden, sämtliche M und F zu addieren und mit den entsprechenden Faktoren c₁ und c₂ zu multiplizieren. Verschiebt man die Linie ein wenig nach oben, so werden alle Bergflächen kleiner, alle Talflächen größer, während die Summe der Massen sich gleichbleibt. Die Transportkosten werden daher am kleinsten, wenn die Summe der F am kleinsten ist, d.h. wenn diese Summe bei einer kleinen Verschiebung der Ausgleichungslinie unverändert bleibt. Diese Bedingung wird erfüllt, wenn die Summe der Berglängen gleich der Summe der Tallängen ist. Durch Probieren läßt sich diese günstigste Lage der Ausgleichungslinie leicht finden. Ist c₂ nicht für alle Abteilungen gleichgroß, so müssen die einzelnen Längen vor der Addition mit den ihnen entsprechenden Faktoren multipliziert werden. Seitenentnahmen und Ablagerungen können im Massennivellement wie folgt berücksichtigt werden: Es sei beispielsweise C' B' D' (Fig. 3) das einem Auftrag entsprechende Stück des Massenprofils; A bezeichne im Grundriß den Mittelpunkt der projektierten Materialgrube, und B sei ein Punkt, über den der Transport der Verhältnisse wegen erfolgen muß. Um diese Seitenentnahme zu berücksichtigen, trägt man nun von B' aus die Strecke A B, von C' aus die Strecke A B + B C und von D' aus die Strecke A B + B D wagerecht auf und verbindet die Endpunkte der aufgetragenen Strecken durch eine stetige Linie. – Erfolgt der Transport durchgängig senkrecht zur Bahnachse, so werden diese Strecken alle gleichgroß und die Kurve C'' B'' D'' läuft parallel zu C' B' D'. Daß der Transport bergauf geht, kann durch eine entsprechende Vergrößerung der Strecke A B berücksichtigt werden. – In ähnlicher Weise kann man Ablagerungen in das Massenprofil eintragen. Das Kostenminimum wird jetzt in der Regel je zwischen zwei aufeinander folgenden Stellen mit Quertransport aufgesucht.

Literatur: Eikemeyer, Das Massennivellement und dessen prakt. Gebrauch, Leipzig 1870; Launhardt, Zeitschr. d. Hannov. Arch.-u. Ing.-Ver. 1874, S. 191; Culmann, Die graph. Statik, 2. Aufl., S. 142, Zürich 1875; Handb. d. Ingenieurwissensch., Bd. 1, 1. Kap., Leipzig 1883; Goering, Massenermittlung, -verteilung und Transportkosten bei Erdarbeiten, 2. Aufl., Berlin 1890.

Mörsch.

Fig. 1.

Fig. 2.

Fig. 3.